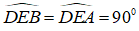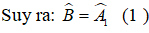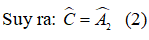cho tam giác ABC vuông tại A,kẻ phân giác BK của góc B(K thuộc AC),kẻ AE vuông góc với BK tại H và E thuộc BC a.chứng minh:AK<KC
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Tham khảo:
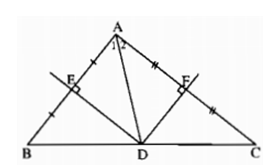
a) Vì D là điểm chung của 2 dường trung trực
=>D là điểm chung của 3 đường trung trực (tính đồng quy trong tam giác)
=>D thuộc trung trực ứng với cạnh BC mà D thuộc BC
=> D là trung điểm của cạnh BC (đpcm)
b) Xét tam giác ADE và BDE có:
DE chung
DA = DB ( vì DE là đường trung trực của AB)
Suy ra: ∆ADE = ∆ BDE ( cạnh huyền – cạnh góc vuông).
+ Chứng minh tương tự ta có: ∆ADF = ∆ CDF ( cạnh huyền – cạnh góc vuông).
Từ (1) và (2) suy ra:

\(\left(-\frac{1}{3}\right)-3=\left(-\frac{1}{3}\right)-\frac{9}{3}=\left(-\frac{10}{3}\right)\)
Nếu sai mong các bạn thông cảm nha.

a, Xét tam giác ADB và tam giác ADC có
AD _ chung ; ^DAB = ^DAC ; AB = AC
Vậy tam giác ADB = tam giác ADC (c.g.c)
b, Xét tam giác ABC cân tại A có AD là phân giác
đồng thời là đường cao hay AD vuông BC
c, Xét tam giác AMD và tam giác AND có
AD _ chung ; ^MAD = ^NAD
Vậy tam giác AMD = tam giác AND ( ch-gn )
=> AM = AN ( 2 cạnh tương ứng )
d, Ta có AM/AB = AN/AC => MN // BC ( Ta lét đảo )

`Answer:`
a. \(25-y^2=8\)
\(\Leftrightarrow y^2=25-8\)
\(\Leftrightarrow y^2=17\)
\(\Leftrightarrow y=\sqrt{17}\)
b. \(x^3y=xy^3+1997\)
\(\Leftrightarrow x^3y-xy^3=1997\)
\(\Leftrightarrow xy\left(x^2-y^2\right)=1997\)
\(\Leftrightarrow xy\left(x+y\right)\left(x-y\right)=1997\)
Ta có:
`1997` là số nguyên tố
`xy(x+y)(x-y)` là hợp số
`=>` Không tìm được `x,y` thoả mãn.
c. \(x+y+9=xy-7\)
\(\Leftrightarrow x-xy+y=-16\)
\(\Leftrightarrow x\left(1-y\right)-1+y=16-1\)
\(\Leftrightarrow x\left(1-y\right)-\left(1-y\right)=-17\)
\(\Leftrightarrow\left(x-1\right)\left(1-y\right)=-17\)
Ta có: \(-17=\left(-17\right).1=1.\left(-17\right)=17.\left(-1\right)=\left(-1\right).17\)
Trường hợp 1: \(\left(x-1\right)\left(1-y\right)=\left(-17\right).1\)
\(\Leftrightarrow\hept{\begin{cases}x=-16\\y=0\end{cases}}\)
Trường hợp 2: \(\left(x-1\right)\left(1-y\right)=1.\left(-17\right)\)
\(\Leftrightarrow\hept{\begin{cases}x=2\\y=18\end{cases}}\)
Trường hợp 3: \(\left(x-1\right)\left(1-y\right)=17.\left(-1\right)\)
\(\Leftrightarrow\hept{\begin{cases}x=18\\y=2\end{cases}}\)
Trường hợp 4: \(\left(x-1\right)\left(1-y\right)=\left(-1\right).17\)
\(\Leftrightarrow\hept{\begin{cases}x=0\\y=-16\end{cases}}\)
Vậy \(\left(x,y\right)=\left(-16,0\right);\left(2,18\right);\left(18,2\right);\left(0,-16\right)\)