7,2 : 2 x 57,2 + 2,86 x 2 x 65 - 25% x 22,88
giải nhanh giúp mình mai mình nộp rồi
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


`#3107.101107`
`x^3 - 4 = 0`
`\Rightarrow x^3 = 4`
`\Rightarrow x =`\(\sqrt[3]{4}\)
Vậy, \(x=\sqrt[3]{4}.\)

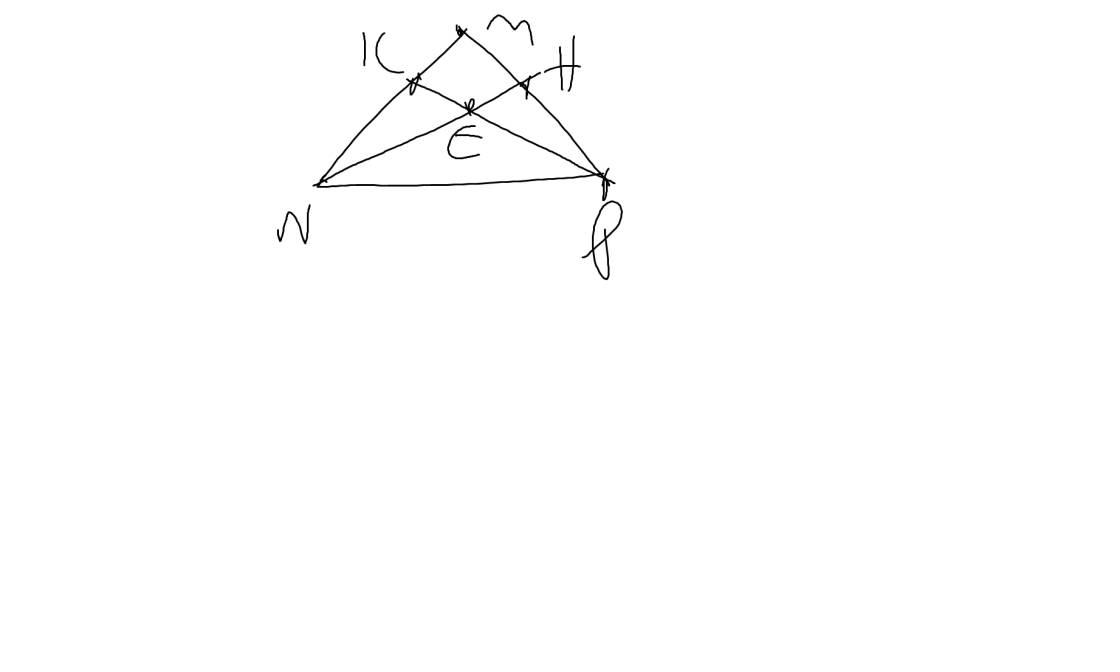
a: Xét ΔKNP vuông tại K và ΔHPN vuông tại H có
NP chung
\(\widehat{KNP}=\widehat{HPN}\)
Do đó: ΔKNP=ΔHPN
b: Xét ΔMNP có
NH,PK là các đường cao
NH cắt PK tại E
Do đó: E là trực tâm của ΔNMP
=>ME\(\perp\)NP

a: Xét ΔHBA vuông tại H và ΔABC vuông tại A có
\(\widehat{HBA}\) chung
Do đó: ΔHBA~ΔABC
=>\(\dfrac{AB}{BC}=\dfrac{HA}{AC}\)
=>\(AB\cdot AC=HA\cdot BC\)
b: Xét ΔAMH vuông tại M và ΔAHB vuông tại H có
\(\widehat{MAH}\) chung
Do đó: ΔAMH~ΔAHB
=>\(\dfrac{AM}{AH}=\dfrac{AH}{AB}\)
=>\(AH^2=AM\cdot AB\left(1\right)\)
Xét ΔANH vuông tại N và ΔAHC vuông tại H có
\(\widehat{NAH}\) chung
Do đó: ΔANH~ΔAHC
=>\(\dfrac{AN}{AH}=\dfrac{AH}{AC}\)
=>\(AN\cdot AC=AH^2\left(2\right)\)
Từ (1),(2) suy ra \(AM\cdot AB=AN\cdot AC\)
=>\(\dfrac{AM}{AC}=\dfrac{AN}{AB}\)
Xét ΔAMN vuông tạiA và ΔACB vuông tại A có
\(\dfrac{AM}{AC}=\dfrac{AN}{AB}\)
Do đó: ΔAMN~ΔACB
c:
ΔABC vuông tại A
=>\(AB^2+AC^2=BC^2\)
=>\(BC=\sqrt{6^2+8^2}=10\left(cm\right)\)
\(AH\cdot BC=AB\cdot AC\)
=>\(AH\cdot10=6\cdot8=48\)
=>AH=48/10=4,8(cm)
ΔABC vuông tại A
=>\(S_{ABC}=\dfrac{1}{2}\cdot AB\cdot AC=\dfrac{1}{2}\cdot6\cdot8=24\left(cm^2\right)\)
Xét tứ giác AMHN có \(\widehat{AMH}=\widehat{ANH}=\widehat{MAN}=90^0\)
nên AMHN là hình chữ nhật
=>MN=AH
mà AH=4,8cm
nên MN=4,8(cm)
ΔAMN~ΔACB
=>\(\dfrac{S_{AMN}}{S_{ACB}}=\left(\dfrac{MN}{CB}\right)^2=\left(\dfrac{4.8}{10}\right)^2\)
=>\(S_{AMN}=\left(\dfrac{4.8}{10}\right)^2\cdot24=5,5296\left(cm^2\right)\)
\(S_{AMN}+S_{BMNC}=S_{ABC}\)
=>\(S_{BMNC}=24-5,5296=18,4704\left(cm^2\right)\)

a: Xét ΔCAB vuông tại A và ΔCAD vuông tại A có
CA chung
AB=AD
Do đó: ΔCAB=ΔCAD
b: ΔCAB=ΔCAD
=>CB=CD
=>ΔCBD cân tại C
AB=AD
=>A là trung điểm của BD
=>\(BD=2\cdot AB=6\left(cm\right)\)
Chu vi tam giác CBD là:
CB+CD+BD
=2CB+2BA
=2(CB+BA)=2(5+3)=16(cm)
c: Xét ΔCDE vuông tại Dvà ΔCBE vuông tại B có
CE chung
CD=CB
Do đó: ΔCDE=ΔCBE
=>ED=EB
=>E nằm trên đường trung trực của DB(1)
Ta có: ΔCDB cân tại C
mà CA là đường cao
nên CA là đường trung trực của DB(2)
Từ (1),(2) suy ra C,A,E thẳng hàng

TK:
Để khai triển biểu thức \((x - 5)^4\), ta có thể sử dụng công thức khai triển Newton hoặc sử dụng quy tắc nhị thức của Pascal. Tuy nhiên, trong trường hợp này, để đơn giản, chúng ta có thể sử dụng quy tắc nhị thức để thực hiện khai triển:
Bằng quy tắc nhị thức, ta có:
\[(x - 5)^4 = \binom{4}{0}x^4(-5)^0 + \binom{4}{1}x^3(-5)^1 + \binom{4}{2}x^2(-5)^2 + \binom{4}{3}x^1(-5)^3 + \binom{4}{4}x^0(-5)^4\]
\(= x^4 + \binom{4}{1}x^3(-5) + \binom{4}{2}x^2(25) + \binom{4}{3}x(-125) + (-5)^4\)
\(= x^4 - 20x^3 + 100x^2 - 500x + 625\)
Vậy kết quả của khai triển biểu thức \((x - 5)^4\) là \(x^4 - 20x^3 + 100x^2 - 500x + 625\).

10% của 1 bộ đồ thể thao là:
280 000 : 100 x 10 = 28 000 (đồng)
20% của 1 hộp bút là:
80 000 : 100 x 20 = 16 000 (đồng)
Tổng số tiền cần trả để mua 1 bộ đồ thể thao và 1 hộp bút khi chưa giảm giá là:
280 000 + 80 000 = 360 000 (đồng)
Khi đã giảm giá, bạn Phúc cần trả:
360 000 - 28 000 - 16 000 = 316 000 (đồng)
Nếu mang theo 400 000 đồng, bạn Phúc còn dư:
400 000 - 316 000 = 84 000 (đồng)
Đáp số: 84 000 đồng

`#3107.101107`
`a)`
`5 - (x - 6) = 4(2x - 3)`
\(\Leftrightarrow5-x+6=8x-12\)
\(\Leftrightarrow-x-8x=-12-5-6\)
\(\Leftrightarrow-9x=-23\)
\(\Leftrightarrow x=\dfrac{-23}{-9}=\dfrac{23}{9}\)
Vậy, \(x=\dfrac{23}{9}\)
`b)`
\(5\left(3x+2\right)-4\left(5-3x\right)=1\)
\(\Leftrightarrow15x+10-20+12x=1\)
\(\Leftrightarrow27x-10=1\)
\(\Leftrightarrow27x=11\)
\(\Leftrightarrow x=\dfrac{11}{27}\)
Vậy, \(x=\dfrac{11}{27}\)
`c)`
\(-4\left(x-3\right)=6x+\left(x-3\right)\)
\(\Leftrightarrow-4x+12=6x+x-3\)
\(\Leftrightarrow-4x-7x=-12-3\)
\(\Leftrightarrow11x=-15\)
\(\Leftrightarrow x=\dfrac{-15}{11}\)
Vậy, \(x=-\dfrac{15}{11}\)
`d)`
\(\dfrac{x}{3}-\dfrac{5x}{6}-\dfrac{5x}{12}=\dfrac{x}{4}-5\)
\(\Leftrightarrow\dfrac{4x}{12}-\dfrac{10x}{12}-\dfrac{5x}{12}=\dfrac{3x}{12}-\dfrac{60}{12}\)
\(\Leftrightarrow4x-10x-5x=3x-60\)
\(\Leftrightarrow-11x-3x=-60\)
\(\Leftrightarrow-14x=-60\)
\(\Leftrightarrow x=\dfrac{-60}{-14}=\dfrac{30}{7}\)
Vậy, \(x=\dfrac{30}{7}\)
`e)`
\(\dfrac{x-1}{2}-\dfrac{x+1}{15}-\dfrac{2x-13}{6}=0\)
\(\Leftrightarrow\dfrac{15\left(x-1\right)}{30}-\dfrac{2\left(x+1\right)}{30}-\dfrac{5\left(2x-13\right)}{30}=0\)
\(\Leftrightarrow15\left(x-1\right)-2\left(x+1\right)-5\left(2x-13\right)=0\)
\(\Leftrightarrow15x-15-2x-2-10x+65=0\)
\(\Leftrightarrow3x+48=0\)
\(\Leftrightarrow3x=-48\)
\(\Leftrightarrow x=-16\)
Vậy, \(x=-16.\)
`f)`
\(\dfrac{3\left(3-x\right)}{8}+\dfrac{2\left(5-x\right)}{3}=\dfrac{1-x}{2}-2\)
\(\Leftrightarrow\dfrac{9\left(3-x\right)}{24}+\dfrac{16\left(5-x\right)}{24}=\dfrac{12\left(1-x\right)}{24}-\dfrac{48}{24}\)
\(\Leftrightarrow27-9x+80-16x=12-12x-48\)
\(\Leftrightarrow-9x-16x+12x=12-48-27-80\)
\(\Leftrightarrow-13x=-143\)
\(\Leftrightarrow x=11\)
Vậy, `x = 11.`
`g)`
\(\dfrac{3\left(5x-2\right)}{4}-2=\dfrac{7x}{3}-5\left(x-7\right)\)
\(\Leftrightarrow\dfrac{9\left(5x-2\right)}{12}-\dfrac{24}{12}=\dfrac{28x}{12}-\dfrac{60\left(x-7\right)}{12}\)
\(\Leftrightarrow45x-18-24=28x-60x+420\)
\(\Leftrightarrow45x-28x+60x=42+420\)
\(\Leftrightarrow77x=462\)
\(\Leftrightarrow x=6\)
Vậy, `x = 6`
`h)`
\(\dfrac{x+5}{2}+\dfrac{3-2x}{4}=x-\dfrac{7+x}{6}\)
\(\Leftrightarrow\dfrac{6\left(x+5\right)}{12}+\dfrac{3\left(3-2x\right)}{12}=\dfrac{12x}{12}-\dfrac{2\left(7+x\right)}{12}\)
\(\Leftrightarrow6x+30+9-6x=12x-14-2x\)
\(\Leftrightarrow-10x=-53\)
\(\Leftrightarrow x=5,3\)
Vậy, `x = 5,3`
`i)`
\(\dfrac{x-3}{11}+\dfrac{x+1}{3}=\dfrac{x+7}{9}-1\)
\(\Leftrightarrow\dfrac{9\left(x-3\right)}{99}+\dfrac{33\left(x+1\right)}{99}=\dfrac{11\left(x+7\right)}{99}-\dfrac{99}{99}\)
\(\Leftrightarrow9x-27+33x+33=11x+77-99\)
\(\Leftrightarrow42x-11x=-22-6\)
\(\Leftrightarrow31x=-28\)
\(\Leftrightarrow x=-\dfrac{28}{31}\)
Vậy, \(x=-\dfrac{28}{31}.\)

7,2:2x57,2+2,86x2x65-25%x22,88
=3,6x57,2+28,6x0,2x65-0,25x22,88
=28,6x(2x3,6+0,2x65)-5,72
=28,6x20,2-5,72
=5,72x(5x20,2-1)
=5,72x100=572