Câu 4:
Cho tam giác ABC vuông tại A. Vẽ về phía ngoài tam giác ABC các tam giác đều ABD và ACE. Gọi I là giao điểm BE và CD. Chứng minh rằng:
1) ΔΑΒΕ = ADC
2) DE = BE
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Các tia đối nhau gốc O là:
Ox;Oy
OA;Oy
OB;Ox
OA;OB
b: Vì OA và OB là hai tia đối nhau
nên O nằm giữa A và B
=>OA+OB=BA
=>OB+3=6
=>OB=3(cm)
Ta có: O nằm giữa A và B
mà OA=OB(=3cm)
nên O là trung điểm của AB
c: 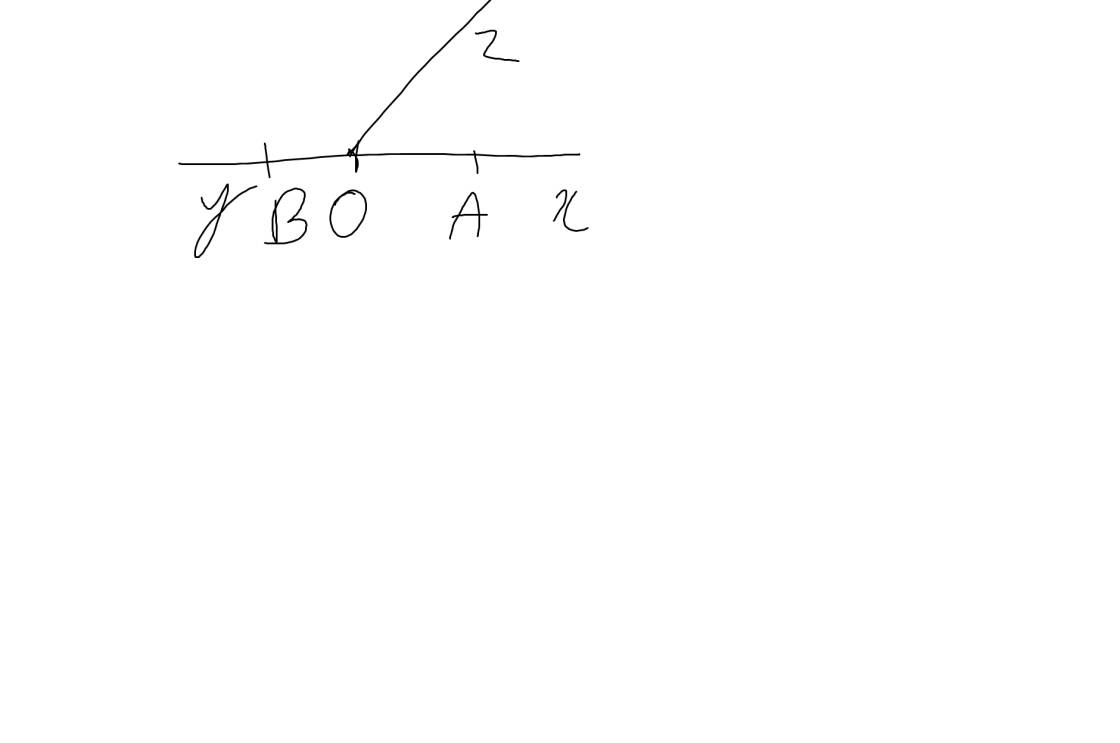

Lời giải:
Hiệu số tuổi của hai bố con không đổi, luôn là $24$ tuổi.
Ba năm trước, coi số tuổi của con là 1 phần thì tuổi của bố là 4 phần.
Hiệu số phần bằng nhau: $4-1=3$ (phần)
Ba năm trước tuổi của con là: $24:3\times 1=8$ (tuổi)
Tuổi con hiện nay: $8+3=11$ (tuổi)
Tuổi bố hiện nay: $11+24=35$ (tuổi)

Thế tích bể là : 5 x 2 x 1 , 2= 12 m 3= 12000 dm3= 12000 lít
Cần phải đổ thêm là : 12000 -( 12000x2/5)=7200 lít
Sử dụng đc trong số ngày là : 12000:600 = 20 ngày = 2 tuần 4 ngày
Vậy sử dụng đc trên 2 tuần vì 2 tuần < 2 tuần 4 ngày

\(\dfrac{-5}{8}\times\dfrac{-12}{29}\times\dfrac{8}{-10}\times5,8\)
\(=-\dfrac{5}{8}\times\dfrac{8}{10}\times5,8\times\dfrac{12}{29}\)
\(=-\dfrac{5}{10}\times\dfrac{29}{5}\times\dfrac{12}{29}\)
\(=-\dfrac{5}{10}\times\dfrac{12}{5}=-\dfrac{12}{10}=-\dfrac{6}{5}\)

a: Các tia đối nhau gốc O là:
Ox;Oy
OA;Oy
OB;Ox
OA;OB
b: Vì OA và OB là hai tia đối nhau
nên O nằm giữa A và B
=>OA+OB=BA
=>OB+3=6
=>OB=3(cm)
Ta có: O nằm giữa A và B
mà OA=OB(=3cm)
nên O là trung điểm của AB
c: 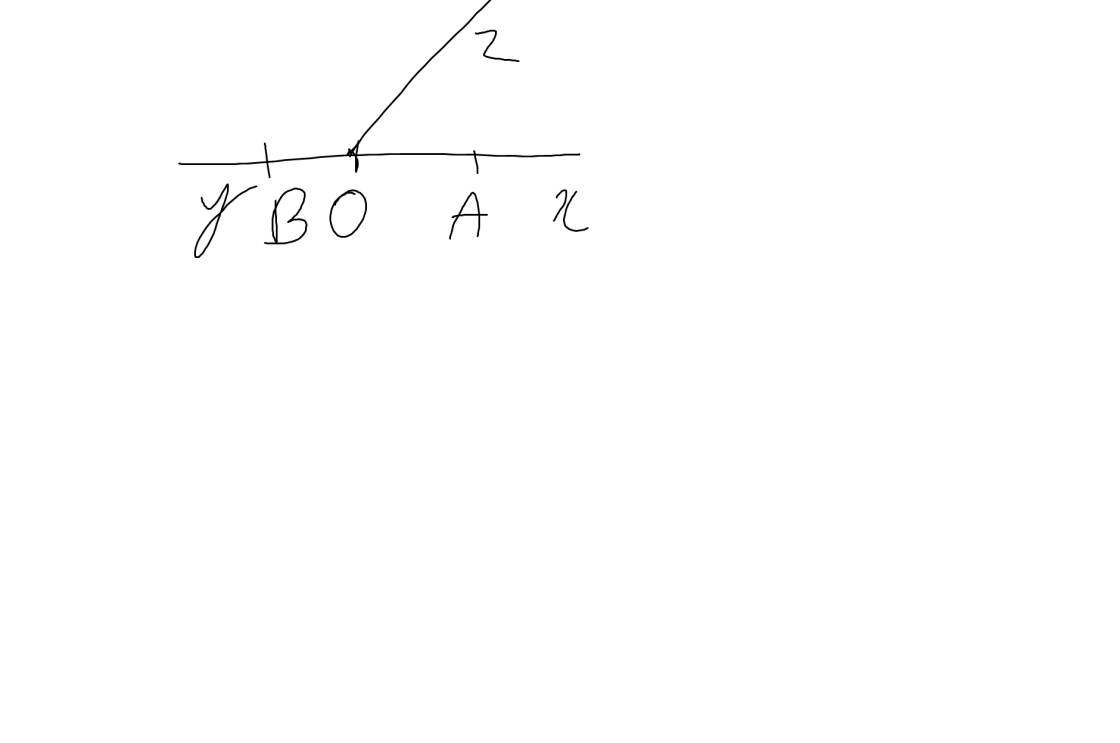

\(\dfrac{-7}{25}+\dfrac{-18}{25}+\dfrac{4}{23}+\dfrac{5}{7}+\dfrac{10}{23}\)
\(=\left(\dfrac{-7}{25}+\dfrac{-18}{25}\right)+\left(\dfrac{4}{23}+\dfrac{10}{23}\right)+\dfrac{5}{7}\)
\(=-1+\dfrac{14}{23}+\dfrac{5}{7}\)
\(=-\dfrac{9}{23}+\dfrac{5}{7}\)
\(=\dfrac{52}{161}\)
\(\dfrac{-7}{25}+\dfrac{-18}{25}+\dfrac{4}{23}+\dfrac{5}{7}+\dfrac{10}{23}\)
\(=\left(-\dfrac{7}{25}-\dfrac{18}{25}\right)+\left(\dfrac{4}{23}+\dfrac{10}{23}\right)+\dfrac{5}{7}\)
\(=-1+\dfrac{14}{23}+\dfrac{5}{7}=-\dfrac{9}{23}+\dfrac{5}{7}=\dfrac{-9\cdot7+5\cdot23}{161}\)
\(=\dfrac{115-63}{161}=\dfrac{52}{161}\)
a) \(\Delta ABD\) đều (gt)
\(\Rightarrow\widehat{DAB}=60^0\)
\(\Rightarrow\widehat{DAC}=\widehat{DAB}+\widehat{BAC}=60^0+90^0=150^0\)
\(\Delta ACE\) đều (gt)
\(\Rightarrow CAE=60^0\)
\(\Rightarrow\widehat{EAB}=\widehat{CAE}+\widehat{BAC}=60^0+90^0=150^0\)
\(\Rightarrow\widehat{EAB}=\widehat{DAC}=150^0\)
Xét \(\Delta ABE\) và \(\Delta ADC\) có:
\(AB=AD\) (do \(\Delta ABD\) đều)
\(\widehat{EAB}=\widehat{DAC}\left(cmt\right)\)
\(AE=AC\) (do \(\Delta ACE\) đều)
\(\Rightarrow\Delta ABE=\Delta ADC\left(c-g-c\right)\)
b) Gọi \(F\) là giao điểm của \(CA\) và \(DE\)
Ta có:
\(\widehat{FAD}=\widehat{FAB}-\widehat{DAB}=\widehat{CAB}-\widehat{DAB}=90^0-60^0=30^0\)
\(\widehat{EAF}+\widehat{CAE}=180^0\) (kề bù)
\(\Rightarrow\widehat{EAF}=180^0-\widehat{CAE}=180^0-60^0=120^0\)
\(\Rightarrow\widehat{EAD}=\widehat{EAF}+\widehat{FAD}=120^0+30^0=150^0\)
\(\Rightarrow\widehat{EAD}=\widehat{EAB}=150^0\)
Xét \(\Delta ADE\) và \(\Delta ABE\) có:
\(AD=AB\left(cmt\right)\)
\(\widehat{EAD}=\widehat{EAB}\left(cmt\right)\)
\(AE\) là cạnh chung
\(\Rightarrow\Delta ADE=\Delta ABE\left(c-g-c\right)\)
\(\Rightarrow DE=BE\) (hai cạnh tương ứng)