Cho đường tròn tâm O, đường kính AB. Gọi C điểm chính giữa cung AB, Điểm D di động trên cung nhỏ AC (D khác A và C). Trên đoạn thẳng BD lấy điểm E sao cho BE = AD, vẽ EH vuông góc với AB (H thuộc AB).
a) Chứng minh Tứ giác ADEH nội tiếp một đường tròn.
b) Chứng minh tam giác CDE vuông cân.
c) Chứng minh đường thẳng vuông góc với BD tại E luôn đi qua một điểm cố định khi D di chuyển trên cung nhỏ AC.

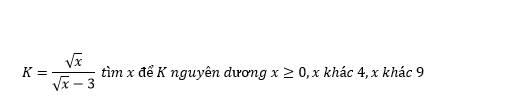

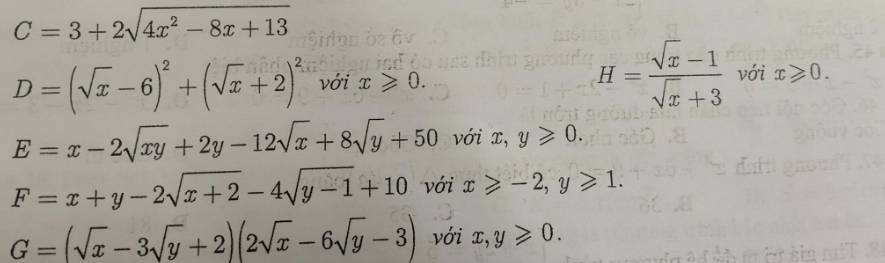

a: Xét (O) có
ΔADB nội tiếp
AB là đường kính
Do đó: ΔADB vuông tại D
Xét tứ giác ADEH có \(\widehat{ADE}+\widehat{AHE}=90^0+90^0=180^0\)
nên ADEH là tứ giác nội tiếp