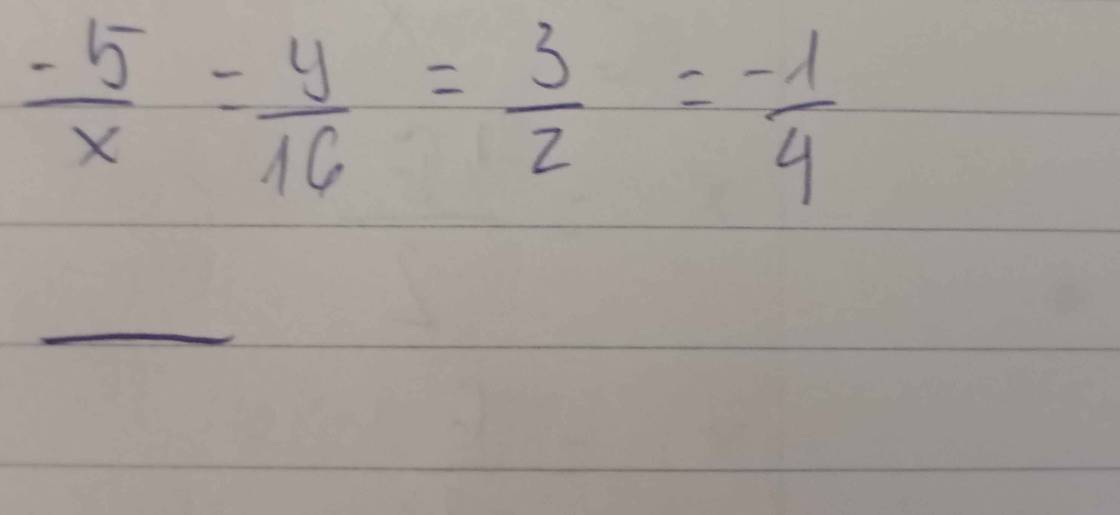 giúp mình với
giúp mình với
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Bài 9:
Quãng đường từ nhà An đến nhà Hà dài:
500-300=200(m)
Bài 6:
C thuộc đoạn AB
=>C nằm giữa A và B
=>CA+CB=AB
=>CB+6=10
=>CB=4(cm)
C là trung điểm của BE
=>\(BE=2\cdot CB=8\left(cm\right)\)
Vì BE<BA
nên E nằm giữa B và A
=>BE+EA=BA
=>EA+8=10
=>EA=2(cm)
C là trung điểm của BE
=>CB=CE
=>CE=4(cm)
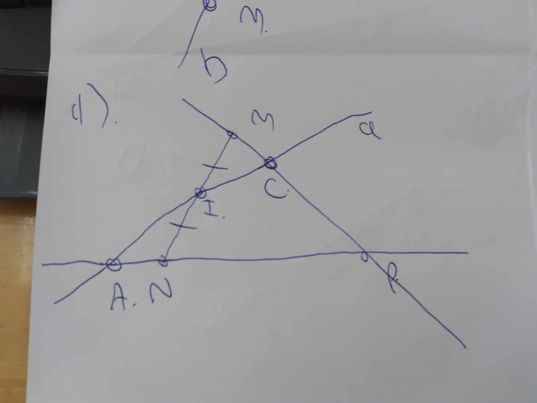

Bài 10:
a) AC > AB (8 > 4)
⇒ B là điểm nằm giữa A và C (1)
\(\Rightarrow AC=AB+BC\)
\(\Rightarrow BC=AC-AB\)
\(\Rightarrow BC=8-4=4\left(cm\right)\)
Ta có: \(BC=AC=4\left(cm\right)\) (2)
Từ (1) và (2)
⇒ B là trung điểm của AC
b) Trên đường thẳng AC lấy điểm D
\(\Rightarrow BC+CD=BD\)
\(\Rightarrow BD=4+3=7\left(cm\right)\)
Bài 9:
Quãng đường từ nhà An đến nhà Hà dài:
500-300=200(m)
Bài 6:
C thuộc đoạn AB
=>C nằm giữa A và B
=>CA+CB=AB
=>CB+6=10
=>CB=4(cm)
C là trung điểm của BE
=>\(BE=2\cdot CB=8\left(cm\right)\)
Vì BE<BA
nên E nằm giữa B và A
=>BE+EA=BA
=>EA+8=10
=>EA=2(cm)
C là trung điểm của BE
=>CB=CE
=>CE=4(cm)

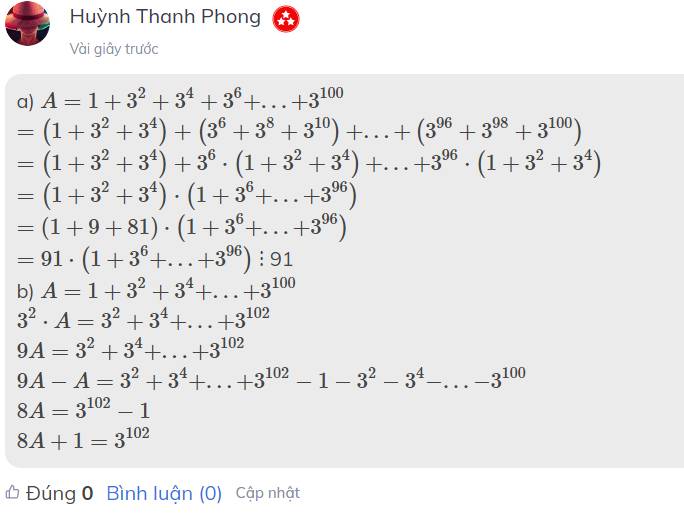
\(8A+1=\left(3^{51}\right)^2\)
⇒ 8A + 1 là một số chính phương

a) \(A=1+3^2+3^4+3^6+...+3^{100}\)
\(=\left(1+3^2+3^4\right)+\left(3^6+3^8+3^{10}\right)+...+\left(3^{96}+3^{98}+3^{100}\right)\)
\(=\left(1+3^2+3^4\right)+3^6\cdot\left(1+3^2+3^4\right)+...+3^{96}\cdot\left(1+3^2+3^4\right)\)
\(=\left(1+3^2+3^4\right)\cdot\left(1+3^6+...+3^{96}\right)\)
\(=\left(1+9+81\right)\cdot\left(1+3^6+...+3^{96}\right)\)
\(=91\cdot\left(1+3^6+...+3^{96}\right)\) ⋮ 91
b) \(A=1+3^2+3^4+...+3^{100}\)
\(3^2\cdot A=3^2+3^4+...+3^{102}\)
\(9A=3^2+3^4+...+3^{102}\)
\(9A-A=3^2+3^4+...+3^{102}-1-3^2-3^4-...-3^{100}\)
\(8A=3^{102}-1\)
\(8A+1=3^{102}\)

\(P=\dfrac{1}{1+2}+\dfrac{1}{1+2+3}+...+\dfrac{1}{1+2+3+...+2023}\)
\(=\dfrac{1}{2\cdot\dfrac{3}{2}}+\dfrac{1}{3\cdot\dfrac{4}{2}}+...+\dfrac{1}{2023\cdot\dfrac{2024}{2}}\)
\(=\dfrac{2}{2\cdot3}+\dfrac{2}{3\cdot4}+...+\dfrac{2}{2023\cdot2024}\)
\(=2\left(\dfrac{1}{2\cdot3}+\dfrac{1}{3\cdot4}+...+\dfrac{1}{2023\cdot2024}\right)\)
\(=2\left(\dfrac{1}{2}-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{4}+...+\dfrac{1}{2023}-\dfrac{1}{2024}\right)\)
\(=2\left(\dfrac{1}{2}-\dfrac{1}{2024}\right)=1-\dfrac{1}{1012}=\dfrac{1011}{1012}\)

Bài 6:
C nằm giữa A và B
=>CA+CB=AB
=>CA+32=60
=>CA=60-32=28(m)
Vậy: Khoảng cách giữa cột C và cột A là 28m
Bài 5:
a: C là trung điểm của AB
=>\(CA=CB=\dfrac{AB}{2}=5\left(cm\right)\)
D thuộc đoạn CA
=>D nằm giữa A và C
=>AD+DC=AC
=>DC+3=5
=>DC=2(cm)
b: E thuộc đoạn CB
=>EC+EB=CB
=>EC+3=5
=>EC=2(cm)
Vì CD và CE là hai tia đối nhau
nên C nằm giữa D và E
mà CD=CE(=2cm)
nên C là trung điểm của DE
Bài 8:
a) Số lần lấy ra bi màu vàng là: 2
Xác suất viên bi lấy ra là bi màu vàng là:
\(\dfrac{2}{8}=\dfrac{1}{4}\)
b) Số lần lấy ra bi không phải màu xanh là: `8-1=7`
Xác suất viên bi lấy ra không phải màu xanh là: `7/8`
c) Số lần lấy ra bi là màu đỏ hoặc tìm là: `3+2=5` (lần)
Xác suất viên bi lấy ra là màu đỏ hoặc tím là: `5/8`

Bài 6:
a: \(\dfrac{3}{4}-x=1\)
=>\(x=\dfrac{3}{4}-1=-\dfrac{1}{4}\)
b: \(x+4=\dfrac{1}{5}\)
=>\(x=\dfrac{1}{5}-4\)
=>\(x=\dfrac{1}{5}-\dfrac{20}{5}=-\dfrac{19}{5}\)
c: \(x-\dfrac{1}{5}=2\)
=>\(x=2+\dfrac{1}{5}\)
=>\(x=\dfrac{11}{5}\)
d: \(\dfrac{x}{-5}=\dfrac{6}{-10}\)
=>\(\dfrac{x}{-5}=\dfrac{3}{-5}\)
=>x=3
Bài 7:
a: 2/3 của 27 là \(\dfrac{2}{3}\cdot27=18\)
b: 5/6 của 300 là \(300\cdot\dfrac{5}{6}=250\)
Bài 5:
e: \(\left(\dfrac{-2}{-5}+\dfrac{-5}{-6}\right)+\dfrac{4}{5}\)
\(=\left(\dfrac{2}{5}+\dfrac{5}{6}\right)+\dfrac{4}{5}\)
\(=\dfrac{6}{5}+\dfrac{5}{6}=\dfrac{61}{30}\)
f: \(\dfrac{5}{13}\cdot\dfrac{17}{26}+\dfrac{5}{13}\cdot\dfrac{9}{26}\)
\(=\dfrac{5}{13}\left(\dfrac{17}{26}+\dfrac{9}{26}\right)\)
\(=\dfrac{5}{13}\cdot\dfrac{26}{26}=\dfrac{5}{13}\)

ĐKXĐ: x<>-1
Để B là số nguyên tố thì \(\left\{{}\begin{matrix}2-3x⋮x+1\\B>0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}-3x-3+5⋮x+1\\\dfrac{2-3x}{x+1}>0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}5⋮x+1\\\dfrac{3x-2}{x+1}< 0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x+1\in\left\{1;-1;5;-5\right\}\\-1< x< \dfrac{2}{3}\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x\in\left\{0;-2;4;-6\right\}\\-1< x< \dfrac{2}{3}\end{matrix}\right.\Leftrightarrow x=0\)
Thay x=0 vào B, ta được:
\(B=\dfrac{2-3\cdot0}{0+1}=\dfrac{2}{1}=2\) là số nguyên tố
Vậy: x=0







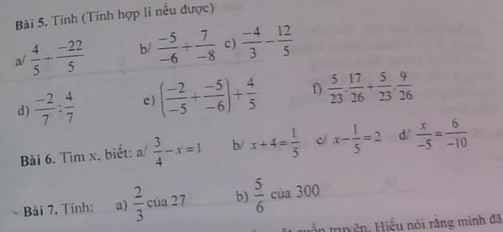
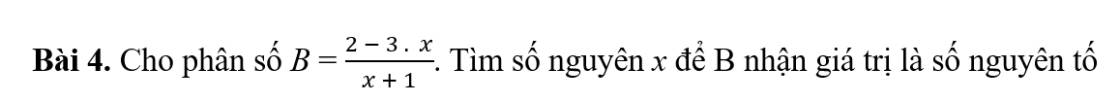
Ta có:
\(\dfrac{-5}{x}=\dfrac{y}{16}=\dfrac{3}{z}=\dfrac{-1}{4}\)
Tìm x:
\(\Rightarrow\dfrac{-5}{x}=\dfrac{-1}{4}\)
\(\Rightarrow\dfrac{-5}{x}=\dfrac{-5}{20}\)
\(\Rightarrow x=20\)
Tìm y:
\(\dfrac{y}{16}=\dfrac{-1}{4}\)
\(\Rightarrow\dfrac{y}{16}=\dfrac{-4}{16}\)
\(\Rightarrow y=-4\)
Tìm z:
\(\dfrac{3}{z}=\dfrac{-1}{4}\)
\(\Rightarrow\dfrac{3}{z}=\dfrac{3}{-12}\)
\(\Rightarrow z=-12\)
Vậy: ....