Bạn xem lại đề nhé, còn thiếu dữ kiện gì nhé

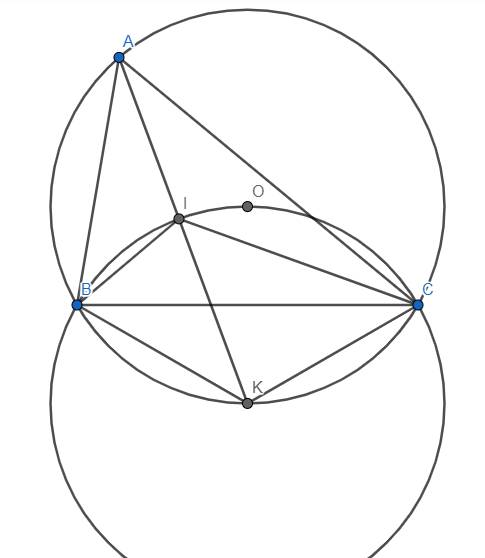
 Gọi (O) là đường tròn ngoại tiếp tam giác ABC, AI cắt (O) tại K. Theo bổ đề quen thuộc thì K là tâm của (BIC). Hơn nữa \(\widehat{BIC}=90^o+\dfrac{\widehat{BAC}}{2}=120^o\) và \(\widehat{BOC}=2\widehat{BAC}=120^o\) nên \(\widehat{BIC}=\widehat{BOC}\), suy ra tứ giác BIOC nội tiếp, suy ra \(O\in\left(K\right)\). Điều này có nghĩa bán kính của \(\left(K\right)\) chính là \(OK=2\).

\(\sqrt[]{x+3}+\sqrt[]{x-1}=2\left(x\ge1\right)\)

\(\Leftrightarrow x+3+x-1+2\sqrt[]{\left(x+3\right)\left(x-1\right)}=4\)

\(\Leftrightarrow2x+2+2\sqrt[]{\left(x+3\right)\left(x-1\right)}=4\)

\(\Leftrightarrow2\sqrt[]{\left(x+3\right)\left(x-1\right)}=4-2\left(x+1\right)\)

\(\Leftrightarrow\sqrt[]{\left(x+3\right)\left(x-1\right)}=2-\left(x+1\right)\)

\(\Leftrightarrow\sqrt[]{\left(x+3\right)\left(x-1\right)}=1-x\)

\(\Leftrightarrow\left\{{}\begin{matrix}1-x\ge0\\\Leftrightarrow\left(x+3\right)\left(x-1\right)=\left(1-x\right)^2\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}x\le1\\\Leftrightarrow x^2+2x-3=x^2-2x+1\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}x\le1\\\Leftrightarrow4x=4\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}x\le1\\\Leftrightarrow x=1\end{matrix}\right.\)

\(\Leftrightarrow x=1\)

Điều kiện xác định: \(x\ge1\)

\(\sqrt{x+3}+\sqrt{x-1}=2\\ \Leftrightarrow x+3+x-1+2\sqrt{\left(x+3\right)\left(x-1\right)}=4\)

\(\Leftrightarrow x+1+\sqrt{x^2+2x-3}=2\\\Leftrightarrow\sqrt{x^2+2x-3}=1-x \)

Để phương trình thỏa mãn thì x\(\le1\)mà \(x\le1\)

\(\Rightarrow x=1\)

Thử lại, ta được: \(\sqrt{1+3}+\sqrt{1-1}=2\left(tm\right)\)

Vậy x=1

ai lm cho mik đi ạ 

Để lập Bảng Bảng Tiến trình (BBT) và vẽ đồ thị cho từng hàm số, ta tiến hành theo các bước sau:

a. y = x^2 - 4x + 3

Đầu tiên, ta lập BBT bằng cách tạo một bảng với các cột cho giá trị của x, giá trị của hàm số y tương ứng và sau đó tính giá trị của y bằng cách thay các giá trị của x vào công thức của hàm số.

-2 | 15 -1 | 8 0 | 3 1 | 0 2 | -1 3 | 0 4 | 3 5 | 8

Sau khi lập BBT, ta có thể vẽ đồ thị bằng cách vẽ các điểm (x, y) tương ứng trên hệ trục tọa độ.

b. y = -x^2 + 2x - 3

Lập BBT:

-2 | -11 -1 | -6 0 | -3 1 | -2 2 | -3 3 | -6 4 | -11

Vẽ đồ thị.

c. y = x^2 + 2x

Lập BBT:

-2 | 0 -1 | 0 0 | 0 1 | 3 2 | 8 3 | 15 4 | 24

Vẽ đồ thị.

d. y = -2x^2 - 2

Lập BBT:

-2 | -6 -1 | -4 0 | -2 1 | -4 2 | -10 3 | -18 4 | -28

Vẽ đồ thị.

Sau khi lập BBT và vẽ đồ thị cho từng hàm số, bạn có thể dễ dàng quan sát và phân tích các đặc điểm của đồ thị như điểm cực trị, đồ thị hướng lên hay hướng xuống, đồ thị cắt trục hoành và trục tung ở những điểm nào, và các đặc tính khác của hàm số.

1) \(\sqrt[]{3x+7}-5< 0\)

\(\Leftrightarrow\sqrt[]{3x+7}< 5\)

\(\Leftrightarrow3x+7\ge0\cap3x+7< 25\)

\(\Leftrightarrow x\ge-\dfrac{7}{3}\cap x< 6\)

\(\Leftrightarrow-\dfrac{7}{3}\le x< 6\)

a.

$x^3-x^2-6x=0$
$\Leftrightarrow x(x^2-x-6)=0$
$\Leftrightarrow x[x(x+2)-3(x+2)]=0$
$\Leftrightarrow x(x+2)(x-3)=0$
$\Leftrightarrow x=0$ hoặc $x+2=0$ hoặc $x-3=0$

$\Leftrightarrow x=0$ hoặc $x=-2$ hoặc $x=3$
Vì $x\in\mathbb{N}^*$ nên $x=3$
Vậy $A=\left\{3\right\}$
------------------------------

b.

$(x^2-x\sqrt{3})(3x^2+5x-2)=0$
$\Leftrightarrow x(x-\sqrt{3})[x(3x-1)+2(3x-1)]=0$

$\Leftrightarrow x(x-\sqrt{3})(3x-1)(x+2)=0$
$\Leftrightarrow x=0$ hoặc $x-\sqrt{3}=0$ hoặc $3x-1=0$ hoặc $x+2=0$

$\Leftrightarrow x\in\left\{0; \sqrt{3}; \frac{1}{3}; -2\right\}$

Vì $x\in\mathbb{Q}$ nên $x\in\left\{0; \frac{1}{3}; -2\right\}$

Vậy $B=\left\{0; \frac{1}{3}; -2\right\}$

c.

$(x-5)^2=49$
$\Leftrightarrow (x-5)^2=7^2=(-7)^2$

$\Leftrightarrow x-5=7$ hoặc $x-5=-7$

$\Leftrightarrow x=12$ hoặc $x=-2$

$x\in\mathbb{N}$ nên $x=12$
Vậy $C=\left\{12\right\}$

-------------------------------

d.

$|x|<5\Leftrightarrow -5< x< 5$

$x\in\mathbb{Z}\Rightarrow x\in\left\{-4; -3; -2; -1; 0; 1; 2;3;4\right\}$
Mà $x^2>5$ nên $x\in\left\{-4; -3; 3; 4\right\}$

Vậy $D=\left\{-4; -3; 3; 4\right\}$

Lời giải:
a.

\(\left\{\begin{matrix} x\neq 0\\ 2x-1\geq 0\\ x^2-3x+2=(x-1)(x-2)\neq 0\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} x\neq 0\\ x\geq \frac{1}{2}\\ x\neq 1; x\neq 2\end{matrix}\right.\)

$\Leftrightarrow x\geq \frac{1}{2}; x\neq 1; x\neq 2$
b. \(\left\{\begin{matrix} x^2-1=(x-1)(x+1)\neq 0\\ 7-2x\geq 0\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} x\neq \pm 1\\ x\leq \frac{7}{2}\end{matrix}\right.\)

c.

\(\left\{\begin{matrix} x\neq 0\\ 4-2x+x^2\neq 0\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} x\neq 0\\ (x-1)^2+3\neq 0\end{matrix}\right.\Leftrightarrow x\neq 0\)

d.

\(\left\{\begin{matrix} 25-x^2=(5-x)(5+x)\geq 0\\ x\geq 0\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} -5\leq x\leq 5\\ x\geq 0\end{matrix}\right.\Leftrightarrow 0\leq x\leq 5\)

a) \(y=\dfrac{1}{x}-\dfrac{\sqrt[]{2x-1}}{x^2-3x+2}\)

Điều kiện \(\) \(2x-1\ge0;x\ne0;x^2-3x+2\ne0\)

\(\Leftrightarrow x\ge\dfrac{1}{2};x\ne0;\left(x-1\right)\left(x-2\right)\ne0\)

\(\Leftrightarrow x\ge\dfrac{1}{2};x\ne0;x\ne1;x\ne2\)