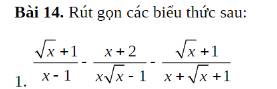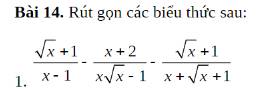Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Với `x >= 0,x \ne 1` có:
`[\sqrt{x}+1]/[x-1]-[x+2]/[x\sqrt{x}-1]-[\sqrt{x}+1]/[x+\sqrt{x}+1]`
`=[\sqrt{x}+1]/[(\sqrt{x}-1)(\sqrt{x}+1)]-[x+2]/[x\sqrt{x}-1]-[\sqrt{x}+1]/[x+\sqrt{x}+1]`
`=1/[\sqrt{x}-1]-[x+2]/[x\sqrt{x}-1]-[\sqrt{x}+1]/[x+\sqrt{x}+1]`
`=[x+\sqrt{x}+1-x-2-(\sqrt{x}+1)(\sqrt{x}-1)]/[(\sqrt{x}-1)(x+\sqrt{x}+1)]`
`=[x+\sqrt{x}+1-x-2-x+1]/[(\sqrt{x}-1)(x+\sqrt{x}+1)]`
`=[-x+\sqrt{x}]/[(\sqrt{x}-1)(x+\sqrt{x}+1)]`
`=[-\sqrt{x}(\sqrt{x}-1)]/[(\sqrt{x}-1)(x+\sqrt{x}+1)]`
`=[-\sqrt{x}]/[\sqrt{x}+1]`

Với x > = 0 ; x khác 4
\(A=\dfrac{9+2x+\sqrt{x}-10-x+1}{x-\sqrt{x}-2}=\dfrac{x+\sqrt{x}}{x-\sqrt{x}-2}=\dfrac{\sqrt{x}}{\sqrt{x}-2}\)
\(=\dfrac{\sqrt{x}-2+2}{\sqrt{x}-2}=1+\dfrac{2}{\sqrt{x}-2}\Rightarrow\sqrt{x}-2\inƯ\left(2\right)=\left\{\pm1;\pm2\right\}\)
| \(\sqrt{x}-2\) | 1 | -1 | 2 | -2 |
| x | 9 | 1 | 16 | 0 |

\(=\dfrac{\sqrt{3}\left(\sqrt{3}+2\right)}{\sqrt{3}}+\dfrac{\sqrt{2}\left(\sqrt{2}+1\right)}{\sqrt{2}+1}-\sqrt{3}+2\)
\(=\sqrt{3}+2+\sqrt{2}-\sqrt{3}+2=4+\sqrt{2}\)