Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Lời giải:
a. Ta thấy $\widehat{BEC}=\widehat{BDC}=90^0$, mà 2 góc này cùng nhìn cạnh $BC$ nên $BEDC$ là tứ giác nội tiếp
$\Rightarrow B,C,D,E$ cùng thuộc 1 đường tròn
b.
Ta thấy $\widehat{AEH}+\widehat{ADH}=90^0+90^0=180^0$ mà 2 góc này là 2 góc đối nhau nên $AEHD$ là tứ giác nội tiếp
$\Rightarrow A,E,H,D$ cùng thuộc 1 đường tròn
c.
$H$ là giao của 2 đường cao $BD, CE$ nên $H$ là trực tâm của tam giác $ABC$
$\Rightarrow AH\perp BC(1)$
Mặt khác: $\widehat{HKC}=90^0$ (góc nt chắn nửa đường tròn đường kính $CH$)
$\Rightarrow HK\perp BC(2)$
Từ $(1); (2)\Rightarrow A,H,K$ thẳng hàng.

Xét đường tròn (O) có AB là đường kính nên \(\widehat{ACB}=90^o\) (góc nội tiếp chắn nửa đường tròn) hay \(BC\perp AE\) tại C hay BC là đường cao của tam giác ABE. Lại có C là trung điểm AB nên BC là trung tuyến của tam giác ABE. Từ đó tam giác ABE cân tại B hay \(BE=BA\). Do BA cố định nên BE không đổi. Mà B cố định nên khi C thay đổi thì E sẽ di chuyển trên đường tròn tâm B, bán kính BA cố định.

\(\widehat{C}=90^o-\widehat{B}=90^o-32^o=58^o\)
\(tanB=\dfrac{AC}{AB}\Leftrightarrow AC=AB.tanB=3,5.tan32^o\left(cm\right)\)
\(cosB=\dfrac{AB}{BC}\Leftrightarrow BC=\dfrac{AB}{cosB}=\dfrac{3,2}{cos32^o}\left(cm\right)\)

\(x^3-x^2-7x+18=4\sqrt{x+2}\) (ĐK: \(x\ge-2\))
\(\Leftrightarrow x^3-x^2-8x+12+x+6-4\sqrt{x+2}=0\)
\(\Leftrightarrow\left(x-2\right)^2\left(x+3\right)+\dfrac{\left(x+6\right)^2-16\left(x+2\right)}{x+6+4\sqrt{x+2}}=0\)
\(\Leftrightarrow\left(x-2\right)^2\left(x+3\right)+\dfrac{x^2-4x+4}{x+6+4\sqrt{x+2}}=0\)
\(\Leftrightarrow\left(x-2\right)^2\left(x+3+\dfrac{1}{x+6+4\sqrt{x+2}}\right)=0\)
\(\Leftrightarrow x-2=0\) (vì \(x\ge-2\))
\(\Leftrightarrow x=2\) (thỏa mãn)

Ta có P = \(x\sqrt{x+y}+y\sqrt{y+z}+z\sqrt{z+x}\)
<=> \(\sqrt{2}P=\sqrt{2}x.\sqrt{x+y}+\sqrt{2}y.\sqrt{y+z}+\sqrt{2}z.\sqrt{z+x}\)
Áp dụng BĐT Cauchy cho 2 số dương \(\sqrt{2}x;\sqrt{x+y}\) được
\(\sqrt{2}x.\sqrt{x+y}\le\dfrac{2x^2+x+y}{2}\)
Tương tự ta được \(\sqrt{2}y.\sqrt{y+z}\le\dfrac{2y^2+y+z}{2}\) ;
\(\sqrt{2}z.\sqrt{z+x}\le\dfrac{2z^2+z+x}{2}\)
Khi đó \(\sqrt{2}P\le\dfrac{2x^2+x+y}{2}+\dfrac{2y^2+y+z}{2}+\dfrac{2z^2+z+x}{2}=3+x+y+z\)
Lại có \(x^2+1\ge2x\) (bđt Cauchy)
\(\Leftrightarrow x\le\dfrac{x^2+1}{2}\)
Tương tự được \(x+y+z\le\dfrac{x^2+1}{2}+\dfrac{y^2+1}{2}+\dfrac{z^2+1}{2}=3\)
Khi đó \(\sqrt{2}P\le3+x+y+z\le6\Leftrightarrow P\le3\sqrt{2}\) (đpcm)
"=" khi x = y = z = 1

Trên tia đối tia CB lấy điểm P sao cho \(CP=CB=b\). Khi đó dễ thấy \(BP=BC+CP=a+b\) . Để ý rằng \(\Delta ACP\) vuông cân tại C nên \(AP=PC\sqrt{2}=b\sqrt{2}\)
Hơn nữa, do CD là tia phân giác của góc BCA vuông nên \(\widehat{BCD}=45^o\), từ đó suy ra CD//AP do có 2 góc đồng vị là \(\widehat{P}\) và \(\widehat{BCD}\) bằng nhau (vì chúng cùng bằng \(45^o\))
Trong tam giác ABP có CD//AP nên \(\dfrac{CD}{AP}=\dfrac{BC}{BP}\) hay \(CD=\dfrac{AP.BC}{BP}=\dfrac{b\sqrt{2}.a}{a+b}=\dfrac{ab}{\left(a+b\right).\dfrac{1}{\sqrt{2}}}=\dfrac{ab}{\left(a+b\right).sin45^o}\) (đpcm)
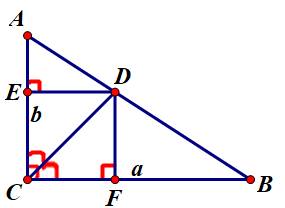
gọi E, F lần lượt là chân đường vuông góc hạ từ D xuống AC, CB.
tứ giác DECF có 3 góc vuông và CD là phân giác góc \(\widehat{ECF}\)
=> DECF là hình vuông
gọi x (đvđd) là cạnh hình vuông DECF, CD là đường chéo hình vuông => CD = \(x\sqrt{2}\) (đvđd)
theo Talet: \(\dfrac{BF}{BC}=\dfrac{DF}{AC}\)hay \(\dfrac{a-x}{a}=\dfrac{x}{b}\Rightarrow ba-bx=ax\Rightarrow ab=x\left(a+b\right)\Rightarrow x=\dfrac{ab}{a+b}\)=> \(CD=x\sqrt{2}=\dfrac{ab}{a+b}\sqrt{2}=\dfrac{ab}{\left(a+b\right).\sin45^o}\) (đpcm)

Lời giải:
ĐKXĐ: $x>1; x\neq 2$
\(B=\frac{\sqrt{x-2\sqrt{x-1}}+\sqrt{x+2\sqrt{x-1}}}{\sqrt{x^2-4x+4}}.\frac{x-2}{x-1}\)
\(=\frac{\sqrt{(x-1)-2\sqrt{x-1}+1}+\sqrt{(x-1)+2\sqrt{x-1}+1}}{\sqrt{(x-2)^2}}.\frac{x-2}{x-1}\)
\(=\frac{\sqrt{(\sqrt{x-1}-1)^2}+\sqrt{(\sqrt{x-1}+1)^2}}{|x-2|}.\frac{x-2}{x-1}\)
\(=\frac{|\sqrt{x-1}-1|+|\sqrt{x-1}+1|}{|x-2|}.\frac{x-2}{x-1}\)
Nêu $x>2$ thì: \(B=\frac{\sqrt{x-1}-1+\sqrt{x-1}+1}{x-2}.\frac{x-2}{x-1}=\frac{2\sqrt{x-1}}{x-2}.\frac{x-2}{x-1}=\frac{2}{\sqrt{x-1}}\)
Nếu $1< x< 2$ thì:
\(B=\frac{1-\sqrt{x-1}+\sqrt{x-1}+1}{2-x}.\frac{x-2}{x-1}=\frac{2}{1-x}\)
b.
TH $1< x< 2$ thì không có giá trị $x$ nguyên nào thỏa mãn
TH $x>2$ thì để $B$ nguyên thì $\sqrt{x-1}$ là ước của $2$
$\Rightarrow \sqrt{x-1}\in \left\{1;2\right\}$
$\Rightarrow x\in \left\{2; 5\right\}$
Vì $x>2$ nên $x=5$
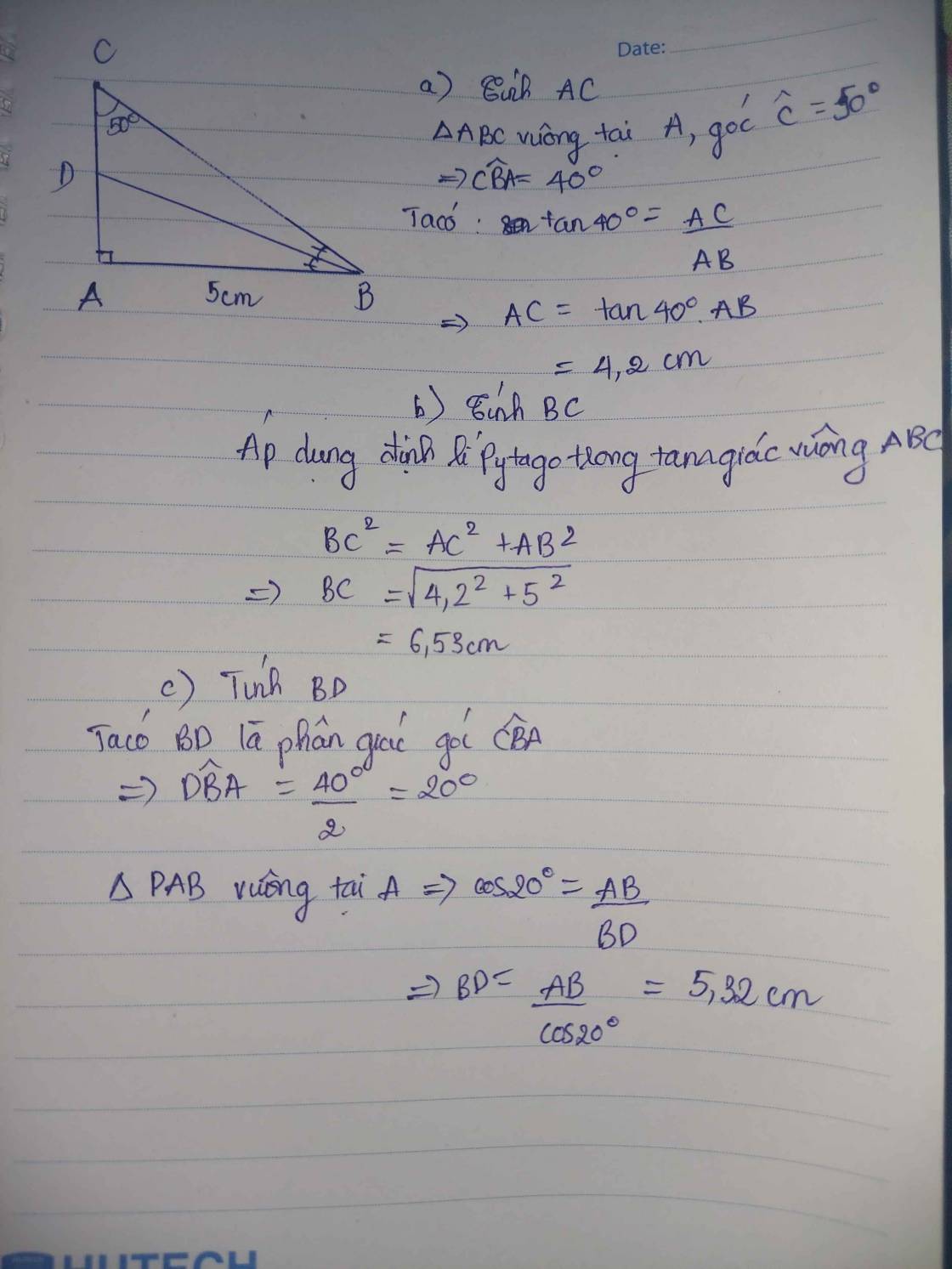
bằng 45
quỹ tích những điểm cách đều 1 điểm O cho trước là đường tròn tâm O