Một hộp có 48 chiếc thẻ cùng loại,mỗi thẻ đc ghi một trong các số 1;2;...48.Hai thẻ khác nhau thì ghi hai số khác nhau.Rút ngẫu nhiên một thẻ trong hộp.Tính xác suất của biến cố "Số xuất hiện trên thẻ đc rút ra là số chính phương"
(Lời giải chi tiết)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

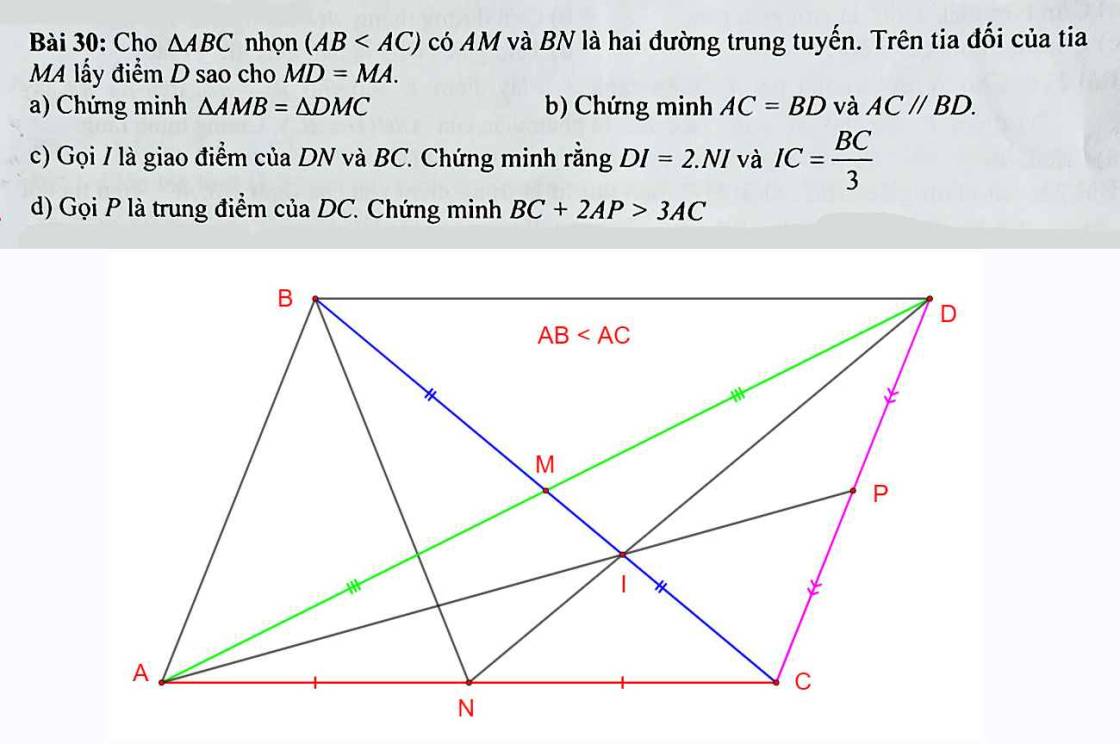
a: Xét ΔAMB và ΔDMC có
MA=MD
\(\widehat{AMB}=\widehat{DMC}\)
MB=MC
Do đó: ΔAMB=ΔDMC
b: Xét ΔMAC và ΔMDB có
MA=MD
\(\widehat{AMC}=\widehat{DMB}\)(hai góc đối đỉnh)
MC=MB
Do đó: ΔMAC=ΔMDB
=>AC=DB
Ta có: ΔMAC=ΔMDB
=>\(\widehat{MAC}=\widehat{MDB}\)
mà hai góc này là hai góc ở vị trí so le trong
nên AC//BD
c: Xét ΔADC có
CM,DN là các đường trung tuyến
CM cắt DN tại I
Do đó: I là trọng tâm của ΔADC
Xét ΔADC có
I là trọng tâm của ΔADC
DN là đường trung tuyến và CM là đường trung tuyến
Do đó: DI=2IN và \(CI=\dfrac{2}{3}CM=\dfrac{2}{3}\cdot\dfrac{1}{2}\cdot BC=\dfrac{1}{3}\cdot BC\)

a: Ta có: ΔABC vuông tại A
=>\(\widehat{ACB}+\widehat{ABC}=90^0\)
=>\(\widehat{ACB}=90^0-50^0=40^0\)
b: Xét ΔCAD và ΔCED có
CA=CE
\(\widehat{ACD}=\widehat{ECD}\)
CD chung
Do đó: ΔCAD=ΔCED
=>DA=DE
c: Ta có: ΔCAD=ΔCED
=>\(\widehat{CAD}=\widehat{CED}\)
mà \(\widehat{CAD}=90^0\)
nên \(\widehat{CED}=90^0\)
=>DE\(\perp\)CB
Xét ΔDAF vuông tại A và ΔDEB vuông tại E có
DA=DE
\(\widehat{ADF}=\widehat{EDB}\)
Do đó: ΔDAF=ΔDEB
=>DF=DB
=>D nằm trên đường trung trực của BF(1)
Ta có: IF=IB
=>I nằm trên đường trung trực của BF(2)
Ta có: CA+AF=CF
CE+EB=CB
mà CA=CE và AF=EB(ΔDAF=ΔDEB)
nên CF=CB
=>C nằm trên đường trung trực của BF(3)
Từ (1),(2),(3) suy ra C,D,I thẳng hàng
a.
Áp dụng tính chất tổng 3 góc trong tam giác:
\(\widehat{ABC}+\widehat{ACB}+\widehat{BAC}=180^0\)
\(\Leftrightarrow50^0+\widehat{ACB}+90^0=180^0\)
\(\Leftrightarrow\widehat{ACB}=40^0\)
b.
Xét hai tam giác DCA và DCE có:
\(\left\{{}\begin{matrix}CA=CE\left(gt\right)\\\widehat{DCA}=\widehat{DCE}\left(\text{CD là phân giác}\right)\\CD\text{ là cạnh chung}\end{matrix}\right.\)
\(\Rightarrow\Delta DCA=\Delta DCE\left(c.g.c\right)\)
\(\Rightarrow DE=DA\)
c.
Từ câu b, do \(\Delta DCA=\Delta DCE\Rightarrow\widehat{DEC}=\widehat{DAC}=90^0\)
Xét hai tam giác CAB và CEF có:
\(\left\{{}\begin{matrix}\widehat{CAB}=\widehat{CEF}=90^0\\CA=CE\left(gt\right)\\\widehat{ACE}-chung\end{matrix}\right.\) \(\Rightarrow\Delta CAB=\Delta CEF\left(g.c.g\right)\)
\(\Rightarrow CB=CF\)
\(\Rightarrow\Delta CBF\) cân tại C
Mà I là trung điểm BF \(\Rightarrow CI\) là trung tuyến nên CI đồng thời là phân giác \(\widehat{ACB}\)
\(\Rightarrow\) Đường thẳng CI trùng đường thẳng AD hay C, D, I thẳng hàng

Bài 2. Tính giá trị của biểu thức:
a) P(3) = 3.3² - 5.3 - 1
= 27 - 16
= 11
P(-3) = 3.(-3)² - 5.(-3) - 1
= 27 + 15 - 1
= 41
b) |x| = 2
⇒ x = 2 hoặc x = -2
Q(2) = 4.2³ - 8.2 + 7
= 32 - 16 + 7
= 23
Q(-2) = 4.(-2)³ - 8.(-2) + 7
= -32 + 16 + 7
= -9
c) Không có giá trị của x nên không tính được
Đa thức một biến
Bài 1.
a) *) 3x⁵ có:
- Hệ số: 3
- Bậc: 5
*) 1/3 x⁷ có:
- Hệ số: 1/3
- Bậc: 7
*) 4x có:
- Hệ số: 4
- Bậc: 1
*) -x³ có:
- Hệ số: -1
- Bậc: 3
b) *) -12x⁹ có:
- Hệ số: -12
- Bậc: 9
*) x³/7 có:
- Hệ số: 1/7
- Bậc: 3
*) -6x có:
- Hệ số: -6
- Bậc: 1
*) 4/19 x³ có:
- Hệ số: 4/19
- Bậc: 3

x : y : z = 3 : 6 : 5
⇒ x/3 = y/6 = z/5
⇒ x²/9 = y²/36 = z²/25
Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:
x²/9 = y²/36 = z²/25 = (x² + y² - z²)/(9 + 36 - 25) = 80/20 = 4
x²/9 = 4 ⇒ x² = 4.9 = 36 ⇒ x = 6; x = -6
*) x = 6
⇒ y = 6.6 : 3 = 12
z = 6.5 : 3 = 10
*) x = -6
⇒ y = -6.6 : 3 = -12
z = -6.5 : 3 = -10
Vậy x = 6; y = 12; z = 10
Hoặc x = -6; y = -12; z = -10


a) Khi rút 1 thẻ thì thẻ đó có thể được đánh số từ 1 đến 12
A = {1; 2; 3; ...; 12}
b) Số xuất hiện trên thẻ là hợp số khi thẻ rút ra được đánh số: 4; 6; 8; 9; 10; 12 nên các kết quả thuận lợi là: 4; 6; 8; 9; 10; 12
c) Số các kết quả thuận lợi cho biến cố trên là 6
Tỉ số của số các kết quả thuận lợi và số phần tử của A là:
6/12 = 1/2
Tập hợp gồm các kết quả có thể xảy ra đối với số xuất hiện trên thẻ được rút ra là: B = {1; 2; 3; …; 11; 12}.
Số phần tử của tập hợp B là: 12 phần tử.
Có 8 kết quả thuận lợi cho biến cố “Số xuất hiện trên thẻ được rút ra là số không chia hết cho 3” là: 1, 2, 4, 5, 7, 8, 10, 11.
Vì thế, xác suất của biến cố “Số xuất hiện trên thẻ được rút ra là số không chia hết cho 3” là: 812=23812=23.

Tỉ lệ nghịch là 2 đại lượng đối nghịch nhau, kiểu như cái này tăng thì cái kia giảm (tc thì xét tích tương ứng). - Tỉ lệ thuận là 2 đại lượng cùng tăng và cùng giảm (tc thì xét tỉ số).

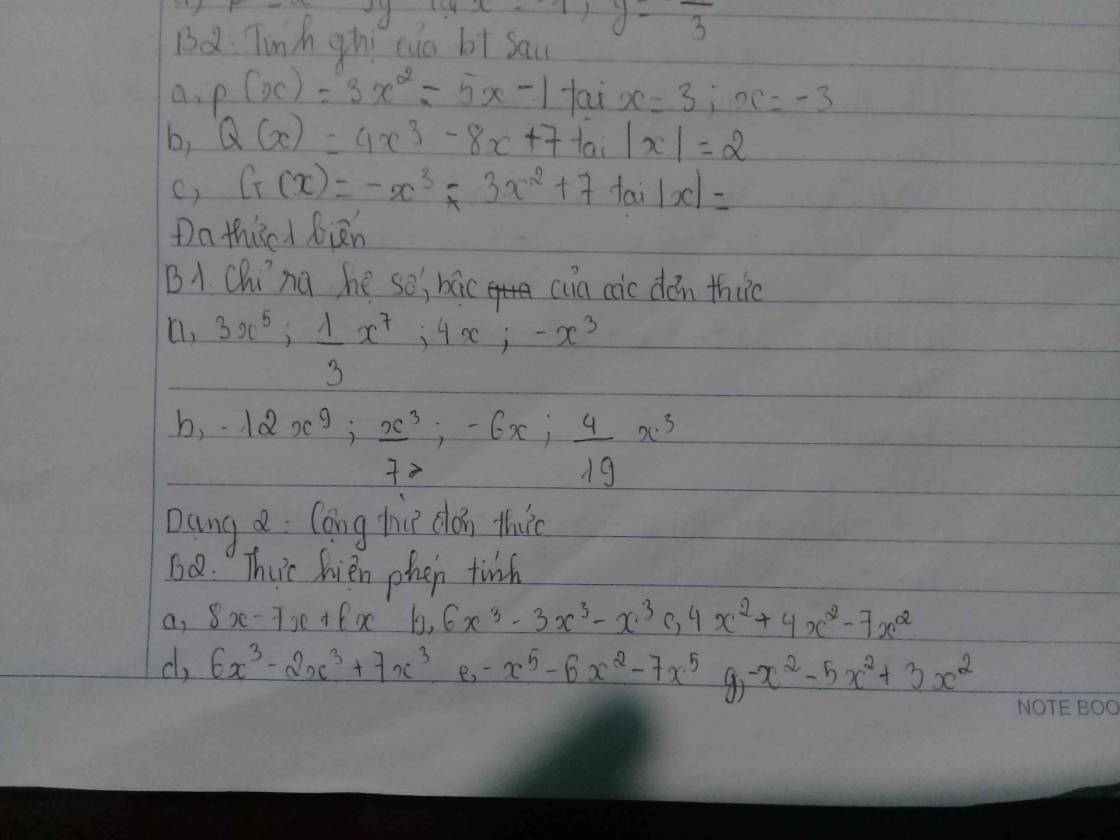


Gọi A là biến cố"Số xuất hiện trên thẻ là số chính phương"
=>A={1;4;9;16;25;36}
=>n(A)=6
=>\(P\left(A\right)=\dfrac{6}{48}=\dfrac{1}{8}\)