Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: \(\dfrac{x^2+5x}{x}=\dfrac{x^2}{x}+\dfrac{5x}{x}=x+5\)
b: \(\dfrac{6x^3-4x^2}{2x^2}=\dfrac{6x^3}{2x^2}-\dfrac{4x^2}{2x^2}=3x-2\)
c: \(\dfrac{8x^2y+6xy}{2xy}=\dfrac{8x^2y}{2xy}+\dfrac{6xy}{2xy}=4x+3\)
d: \(\left(x^2-x+3\right)\left(x-2\right)\)
\(=x^3-2x^2-x^2+2x+3x-6\)
\(=x^3-3x^2+5x-6\)
e: \(\dfrac{8x^3y}{4xy}=\dfrac{8}{4}\cdot\dfrac{x^3}{x}\cdot\dfrac{y}{y}=2x^2\)
f: \(\left(-4xy^2\right)\cdot\left(-\dfrac{1}{4}x\right)=\left(-4\right)\cdot\left(-\dfrac{1}{4}\right)\cdot x\cdot x\cdot y^2=x^2y^2\)
g: \(\dfrac{x^4-2x^2+1}{x-1}\)
\(=\dfrac{\left(x^2-1\right)^2}{x-1}=\dfrac{\left[\left(x-1\right)\left(x+1\right)\right]^2}{\left(x-1\right)}\)
\(=\dfrac{\left(x-1\right)^2\cdot\left(x+1\right)^2}{\left(x-1\right)}=\left(x-1\right)\left(x+1\right)^2\)
Lời giải:
a. $(x^2+5x):x=x(x+5):x=x+5$
b. $(6x^4-4x^2):(2x^2)=2x^2(3x^2-2):(2x^2)=3x^2-2$
c. $(8x^2y+6xy):(2xy)=2xy(4x+3):(2xy)=4x+3$
d.
$(x^2-x+3)(x-2)=x(x^2-x+3)-2(x^2-x+3)$
$=x^3-x^2+3x-2x^2+2x-6=x^3-3x^2+5x-6$
e.
$(8x^3y):(4xy)=2x^2$
f.
$(-4xy^2).\frac{-1}{4}x=x^2y^2$
g.
$(x^4-2x^2+1):(x-1)=(x^2-1)^2:(x-1)=(x-1)^2(x+1)^2:(x-1)=(x-1)(x+1)^2$

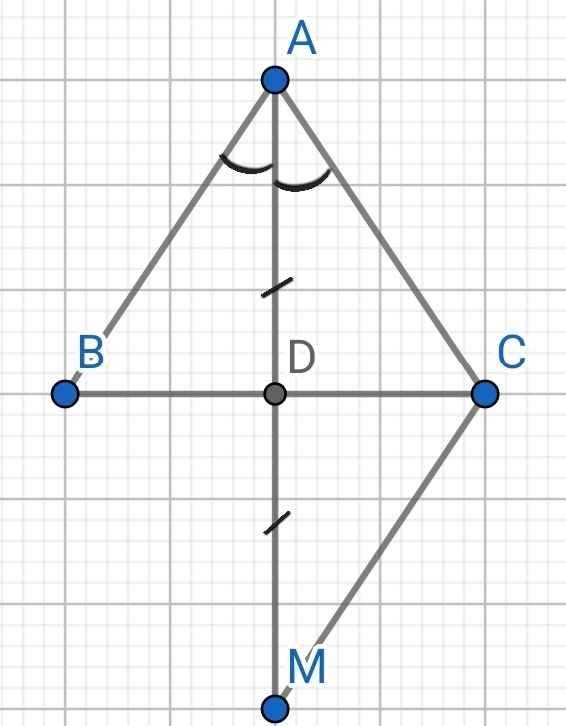
a) Sửa đề: Chứng minh ∆ABD = ∆MCD
Do ∆ABC cân tại A (gt)
AD là tia phân giác của ∠BAC (gt)
⇒ AD là đường trung tuyến của ∆ABC
⇒ D là trung điểm của BC
⇒ BD = CD
Xét ∆ABD và ∆MCD có:
AD = MD (gt)
BD = CD (cmt)
∠ADB = ∠MDC (đối đỉnh)
⇒ ∆ABD = ∆MCD (c-g-c)
b) Do ∆ABD = ∆MCD (cmt)
⇒ ∠ABD = ∠MCD (hai góc tương ứng)
Mà ∠ABD và ∠MCD là hai góc so le trong
⇒ AB // CM
c) Do ∆ABC cân tại A (gt)
⇒ AB = AC
Do ∆ABD = ∆MCD (cmt)
⇒ AB = CM
Mà AB = AC (cmt)
⇒ AC = CM

\(M\left(x\right)=2x^2+3x-5=0\\ \Leftrightarrow2x^2-2x+5x-5=0\\ \Leftrightarrow2x\left(x-1\right)+5\left(x-1\right)=0\\ \Leftrightarrow\left(2x+5\right)\left(x-1\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}2x+5=0\\x-1=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-\dfrac{5}{2}\\x=1\end{matrix}\right.\)
Đa thức có 2 nghiệm là x= -5/2 ; x=1

\(C=x^2+2x.\left(3y-5\right)+\left(3y-5\right)^2-6xy+26\)
\(=x^2+6xy-10x+\left(3y-5\right)^2-6xy+26\)
\(=x^2-10x+25+\left(3y-5\right)^2+1\)
\(=\left(x-5\right)^2+\left(3y-5\right)^2+1\)
Do \(\left\{{}\begin{matrix}\left(x-5\right)^2\ge0\\\left(3y-5\right)^2\ge0\end{matrix}\right.\) ; \(\forall x;y\)
\(\Rightarrow C\ge1\)
Vậy \(C_{min}=1\) khi \(\left\{{}\begin{matrix}x=5\\y=\dfrac{5}{3}\end{matrix}\right.\)

a: \(H\left(x\right)=F\left(x\right)+G\left(x\right)\)
\(=x^4+x^3-3x^2+2x-9-x^4+2x^2-x+8\)
\(=x^3-x^2+x-1\)
\(K\left(x\right)=F\left(x\right)-G\left(x\right)\)
\(=x^4+x^3-3x^2+2x-9+x^4-2x^2+x-8\)
\(=2x^4+x^3-5x^2+3x-17\)
b: \(H\left(0\right)=0^3-0^2+0-1=-1\)
=>x=0 không là nghiệm của H(x)
\(H\left(1\right)=1^3-1^2+1-1=0\)
=>x=1 là nghiệm của H(x)
\(H\left(-1\right)=\left(-1\right)^3-\left(-1\right)^2+\left(-1\right)-1=1-1-1-1=-2\)
=>x=-1 không là nghiệm của H(x)
c: G(x)-M(x)=2x2
=>\(M\left(x\right)=G\left(x\right)-2x^2=-x^4+2x^2-x+8-2x^2\)
\(=-x^4-x+8\)

\(M=-1-2x^2\)
Ta thấy \(x^2\ge0\forall x\)
\(\Rightarrow-2x^2\le0\forall x\)
\(\Rightarrow-1-2x^2\le-1\forall x\Rightarrow M\le-1\forall x\)
hay \(M< 0\forall x\)
------------------------------------------------
\(N=4x-x^2-5\)
\(=-\left(x^2-4x+4\right)-1\)
\(=-\left(x-2\right)^2-1\)
Ta thấy: \(\left(x-2\right)^2\ge0\forall x\)
\(\Rightarrow-\left(x-2\right)^2\le0\forall x\)
\(\Rightarrow-\left(x-2\right)^2-1\le-1\forall x\Rightarrow N\le-1\forall x\)
hay \(N< 0\forall x\)
------------------------------------------------
\(P=6x-x^2-10\)
\(=-\left(x^2-6x+9\right)-1\)
\(=-\left(x-3\right)^2-1\)
Ta thấy: \(\left(x-3\right)^2\ge0\forall x\)
\(\Rightarrow-\left(x-3\right)^2\le0\forall x\)
\(\Rightarrow-\left(x-3\right)^2-1\le-1\forall x\Rightarrow P\le-1\forall x\)
hay \(P< 0\forall x\)
------------------------------------------------
\(Q=4x-x^2+3\)
\(=-\left(x^2-4x+4\right)+7\)
\(=-\left(x-2\right)^2+7\)
Ta thấy: \(\left(x-2\right)^2\ge0\forall x\)
\(\Rightarrow-\left(x-2\right)^2\le0\forall x\)
\(\Rightarrow-\left(x-2\right)^2+7\le7\forall x\Rightarrow Q\le7\forall x\)
*Bạn xem lại đề bài nhé*
------------------------------------------------
\(U=-x^2+x-1\)
\(=-\left(x^2-x\right)-1\)
\(=-\left[x^2-2\cdot x\cdot\dfrac{1}{2}+\left(\dfrac{1}{2}\right)^2\right]+\dfrac{1}{4}-1\)
\(=-\left(x-\dfrac{1}{2}\right)^2-\dfrac{3}{4}\)
Ta thấy: \(\left(x-\dfrac{1}{2}\right)^2\ge0\forall x\)
\(\Rightarrow-\left(x-\dfrac{1}{2}\right)^2\le0\forall x\)
\(\Rightarrow-\left(x-\dfrac{1}{2}\right)^2-\dfrac{3}{4}\le-\dfrac{3}{4}\forall x\Rightarrow U\le-\dfrac{3}{4}\forall x\)
hay \(U< 0\forall x\)
\(Toru\)
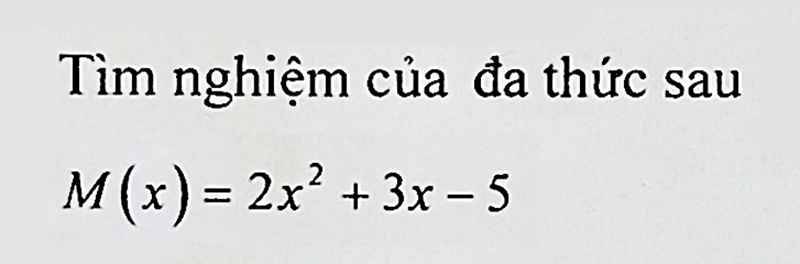
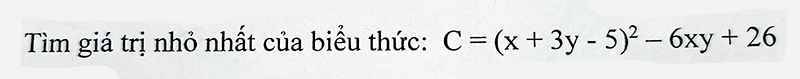
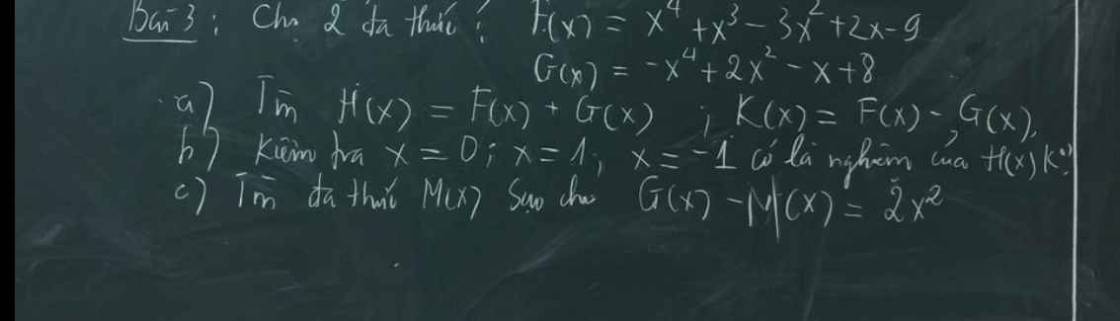
Đặt K(x)=0
=>\(4\left(x+3\right)-x\left(x+1\right)-12=0\)
=>\(4x+12-x^2-x-12=0\)
=>\(-x^2+3x=0\)
=>\(-x\left(x-3\right)=0\)
=>\(\left[{}\begin{matrix}x=0\\x=3\end{matrix}\right.\)