
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


một bao gạo là :
20:1x4 bằng 80 kg
Đáp án là :
80x3:5 bằng 48 kg
Bao gạo đó có cân nặng là:
`20:1/4=80(kg)`
3/5 bao gạo đó có cân nặng là:
`3/5 xx 80 = 48(kg)`
ĐS: ...

Bài 3:
\(a,x-\dfrac{2}{5}=0,24\\ =>x-\dfrac{2}{5}=\dfrac{6}{25}\\ =>x=\dfrac{6}{25}+\dfrac{2}{5}\\ =>x=\dfrac{16}{25}\\ b,\left(\dfrac{7}{3}x-0,6\right):3\dfrac{2}{5}=1\\ =>\left(\dfrac{7}{3}x-\dfrac{3}{5}\right):\dfrac{17}{5}=1\\ =>\dfrac{7}{3}x-\dfrac{3}{5}=\dfrac{17}{5}\\ =>\dfrac{7}{3}x=\dfrac{17}{5}+\dfrac{3}{5}=4\\ =>x=4:\dfrac{7}{3}=\dfrac{12}{7}\\ c,\left(2\dfrac{4}{5}x-50\right):\dfrac{2}{3}=51\\ =>\dfrac{14}{5}x-50=\dfrac{2}{3}\cdot51=34\\ =>\dfrac{14}{5}x=34+50=84\\ =>x=84:\dfrac{14}{5}=30\)
Bài 4:
a: \(5\dfrac{4}{7}:x=13\)
=>\(\dfrac{39}{7}:x=13\)
=>\(x=\dfrac{39}{7}:13=\dfrac{3}{7}\)
b: \(6\dfrac{2}{9}x+3\dfrac{10}{27}=22\dfrac{1}{7}\)
=>\(\dfrac{56}{9}x=22+\dfrac{1}{7}-3-\dfrac{10}{27}=19+\dfrac{-43}{189}=\dfrac{3548}{189}\)
=>\(x=\dfrac{3548}{189}:\dfrac{56}{9}=\dfrac{887}{294}\)
c: \(\left(\dfrac{7}{3}x-0,6\right):3\dfrac{2}{5}=1\)
=>\(\left(\dfrac{7}{3}x-0,6\right)=1\cdot3\dfrac{2}{5}=3,4\)
=>\(\dfrac{7}{3}x=3,4+0,6=4\)
=>\(x=4:\dfrac{7}{3}=\dfrac{12}{7}\)
d: \(\left(2\dfrac{4}{5}x-50\right):\dfrac{2}{3}=51\)
=>\(\left(2,8x-50\right)=51\cdot\dfrac{2}{3}=34\)
=>2,8x=34+50=84
=>\(x=\dfrac{84}{2,8}=30\)
e:
\(\left(4\dfrac{1}{2}-2x\right)\cdot3\dfrac{2}{3}=\dfrac{11}{15}\)
=>\(\left(\dfrac{9}{2}-2x\right)\cdot\dfrac{11}{3}=\dfrac{11}{15}\)
=>\(\dfrac{9}{2}-2x=\dfrac{11}{15}:\dfrac{11}{3}=\dfrac{3}{15}=\dfrac{1}{5}\)
=>\(2x=\dfrac{9}{2}-\dfrac{1}{5}=\dfrac{45}{10}-\dfrac{2}{10}=\dfrac{43}{10}\)
=>\(x=\dfrac{43}{20}\)

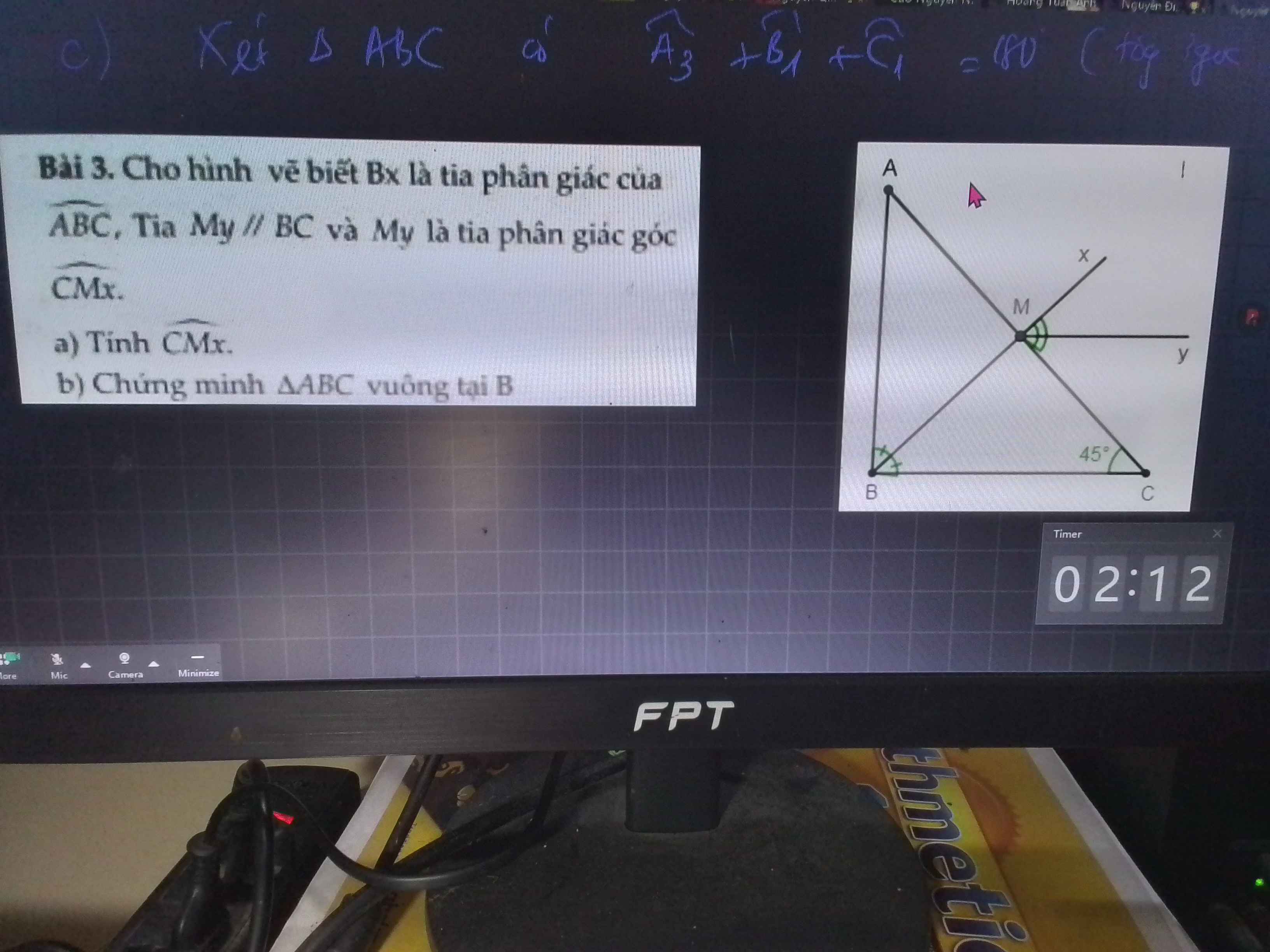
a.
Do \(My||BC\Rightarrow\widehat{CMy}=\widehat{MCB}\) (so le trong)
Mà \(\widehat{MCB}=45^0\Rightarrow\widehat{CMy}=45^0\)
lại có My là phân giác của \(\widehat{CMx}\Rightarrow\widehat{CMx}=2\widehat{CMy}\)
\(\Rightarrow\widehat{CMx}=2.45^0=90^0\)
b.
Do \(BC||My\Rightarrow\widehat{CBM}=\widehat{xMy}\)
Mà \(\widehat{xMy}=\widehat{CMy}=45^0\) (My là phân giác)
\(\Rightarrow\widehat{CBM}=45^0\)
Lại có Bx là phân giác \(\widehat{ABC}\Rightarrow\widehat{ABC}=2\widehat{CBM}\)
\(\Rightarrow\widehat{ABC}=2.45^0=90^0\)
\(\Rightarrow\Delta ABC\) vuông tại B

Áp dụng công thức: \(1+2+...+n=\dfrac{n\left(n+1\right)}{2}\)
\(\Rightarrow1-\dfrac{1}{1+2+...+n}=1-\dfrac{1}{\dfrac{n\left(n+1\right)}{2}}=1-\dfrac{2}{n\left(n+1\right)}\)
\(=\dfrac{n\left(n+1\right)-2}{n\left(n+1\right)}=\dfrac{n^2+n-2}{n\left(n+1\right)}=\dfrac{\left(n-1\right)\left(n+2\right)}{n\left(n+1\right)}\)
Do đó:
\(A=\dfrac{1.4}{2.3}.\dfrac{2.5}{3.4}.\dfrac{3.6}{4.5}...\dfrac{\left(n-1\right)\left(n+2\right)}{n\left(n+1\right)}\)
\(=\dfrac{1.2.3...\left(n-1\right)}{2.3.4...n}.\dfrac{4.5.6...\left(n+2\right)}{3.4.5...\left(n+1\right)}=\dfrac{1}{n}.\dfrac{n+2}{3}=\dfrac{n+2}{3n}\)
\(\Rightarrow A=\dfrac{B}{3}\)
\(\Rightarrow\dfrac{A}{B}=\dfrac{1}{3}\)

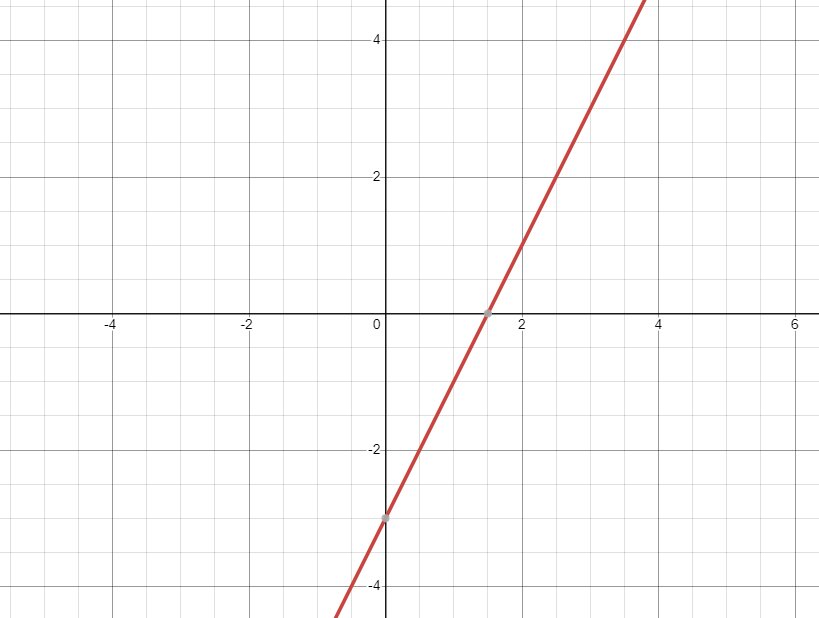
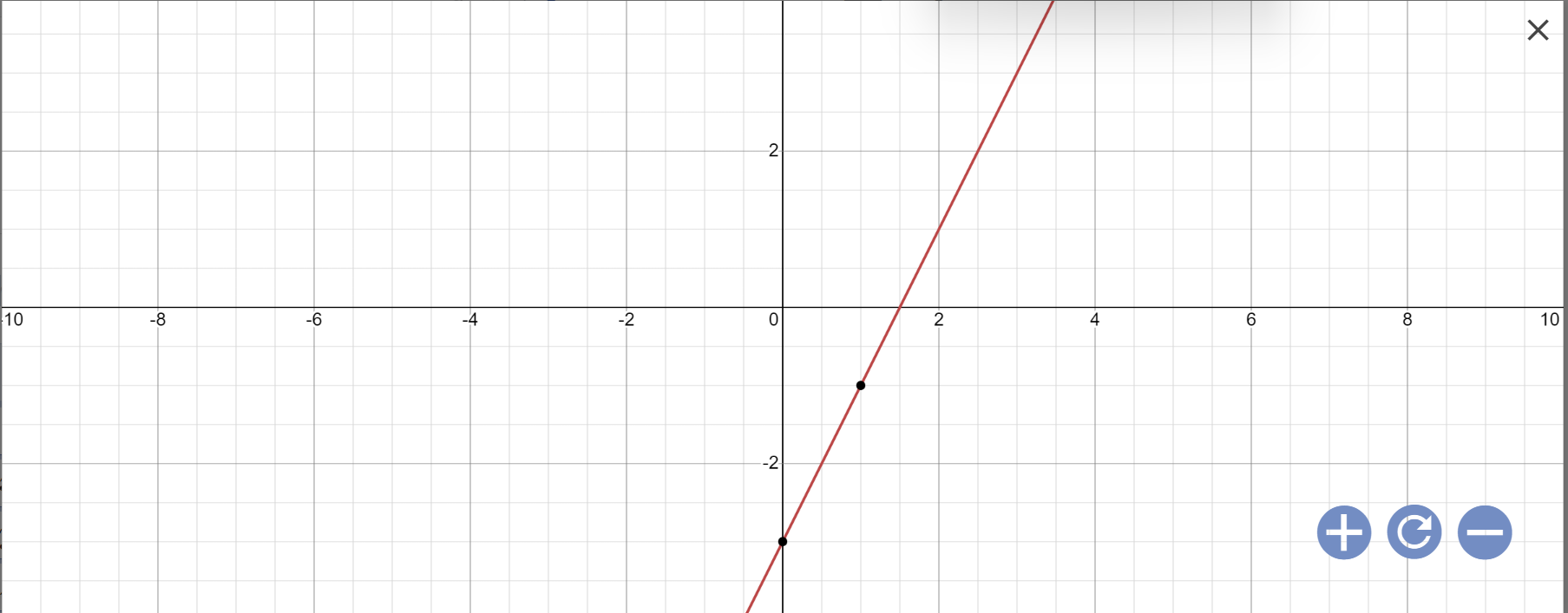
Đồ thị hàm số cắt Ox tại: `(3/2;0)`
Đồ thị hàm số cắt Oy tại `(0;-3)
Vẽ đồ thị hàm số:

a: X,Y trái dấu
=>XY<0
=>\(-2abc^3\cdot3a^2b^3c^5< 0\)
=>\(-6a^3b^4c^8< 0\)
=>\(a^3>0\)
=>a>0
b: X,Y cùng dấu
=>X*Y>0
=>\(-2abc^3\cdot3a^2b^3c^5>0\)
=>\(-6a^3b^4c^8>0\)
=>\(a^3< 0\)
=>a<0
c: \(X\cdot Y=-5a^2n\cdot b\cdot3a^4n\cdot b^5=-15a^6n^2b^6< =0\forall a,b,n\)
=>X và Y không thể cùng có giá trị âm

a: \(5^{56}=\left(5^7\right)^8=78125^8\)
\(11^{24}=\left(11^3\right)^8=1331^8\)
mà 78125>1331
nên \(5^{56}>11^{24}\)
b: \(5^{23}=5\cdot5^{22}< 6\cdot5^{22}\)
c:
\(7\cdot2^{13}< 8\cdot2^{13}=2^3\cdot2^{13}=2^{16}\)

a: \(\dfrac{21}{25}\cdot\dfrac{11}{9}\cdot\dfrac{5}{7}=\dfrac{21}{7}\cdot\dfrac{5}{25}\cdot\dfrac{11}{9}\)
\(=3\cdot\dfrac{11}{9}\cdot\dfrac{1}{5}=\dfrac{11}{3}\cdot\dfrac{1}{5}=\dfrac{11}{15}\)
b: \(\dfrac{5}{23}\cdot\dfrac{17}{26}+\dfrac{5}{23}\cdot\dfrac{9}{26}\)
\(=\dfrac{5}{23}\left(\dfrac{17}{26}+\dfrac{9}{26}\right)\)
\(=\dfrac{5}{23}\cdot1=\dfrac{5}{23}\)
c: \(\dfrac{7}{13}\cdot\dfrac{5}{19}+\dfrac{7}{19}\cdot\dfrac{8}{13}-3\dfrac{7}{19}\)
\(=\dfrac{7}{19}\left(\dfrac{5}{13}+\dfrac{8}{13}\right)-3-\dfrac{7}{19}\)
\(=\dfrac{7}{19}-3-\dfrac{7}{19}=-3\)
\(a,\dfrac{21}{25}.\dfrac{11}{9}.\dfrac{5}{7}\)
\(=\dfrac{21.11.5}{25.9.7}\)
\(=\dfrac{1.11.1}{5.3.1}\)
\(=\dfrac{11}{15}\)
\(b,\dfrac{5}{23}.\dfrac{17}{26}+\dfrac{5}{23}.\dfrac{9}{26}\)
\(=\dfrac{5}{23}.\left(\dfrac{17}{26}+\dfrac{9}{26}\right)\)
\(=\dfrac{5}{23}.1\)
\(=\dfrac{5}{23}\)
\(c,\dfrac{7}{13}.\dfrac{5}{19}+\dfrac{7}{19}.\dfrac{8}{13}\)
\(=\dfrac{7}{19}.\dfrac{5}{13}+\dfrac{7}{19}.\dfrac{8}{13}\)
\(=\dfrac{7}{19}.\left(\dfrac{5}{13}+\dfrac{8}{13}\right)\)
\(=\dfrac{7}{19}.1\)
\(=\dfrac{7}{19}\)

a: m\(\perp\)a
n\(\perp\)a
Do đó: m//n
b: m//n
=>\(\widehat{A_1}=\widehat{ABC}\)(hai góc so le trong)
=>\(\widehat{A_1}=72^0\)
c: Xét ΔABC có \(\widehat{BAC}+\widehat{ACB}+\widehat{ABC}=180^0\)
=>\(\widehat{C_1}=180^0-64^0-72^0=44^0\)
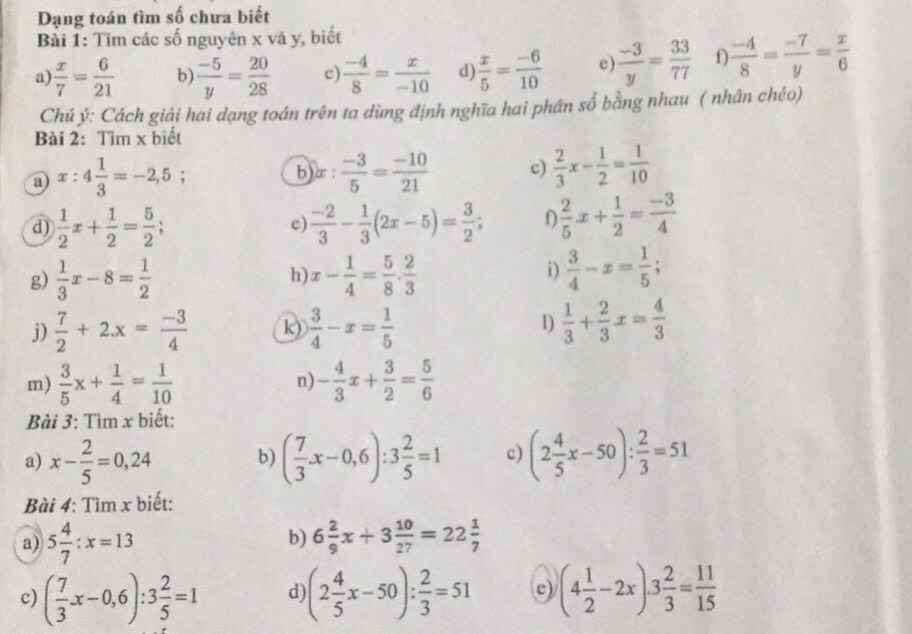



a: Xét ΔNAM và ΔNCP có
NA=NC
\(\widehat{ANM}=\widehat{CNP}\)(hai góc đối đỉnh)
NM=NP
Do đó: ΔNAM=ΔNCP
=>\(\widehat{NAM}=\widehat{NCP}\)
=>CP//AM
=>CP//AB
b: Xét ΔNAP và ΔNCM có
NA=NC
\(\widehat{ANP}=\widehat{CNM}\)(hai góc đối đỉnh)
NP=NM
Do đó: ΔNAP=ΔNCM
=>\(\widehat{NAP}=\widehat{NCM}\)
=>AP//CM
c: Xét ΔABC có
M,N lần lượt là trung điểm của AB,AC
=>MN là đường trung bình của ΔABC
=>MN//BC và \(MN=\dfrac{BC}{2}\)
Ta có: BC=2MN
mà MP=2MN
nên BC=MP
Ta có: ΔNAM=ΔNCP
=>AM=CP
=>CP=BM
Xét ΔMBC và ΔCPM có
MB=CP
BC=PM
MC chung
Do đó: ΔMBC=ΔCPM