
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: ΔABC vuông tại A
=>\(\widehat{ABC}+\widehat{ACB}=90^0\)
=>\(\widehat{ACB}=90^0-55^0=35^0\)
Xét ΔABC có \(\widehat{ACB}< \widehat{ABC}\)
mà AB,AC lần lượt là cạnh đối diện của các góc ACB,ABC
nên AB<AC
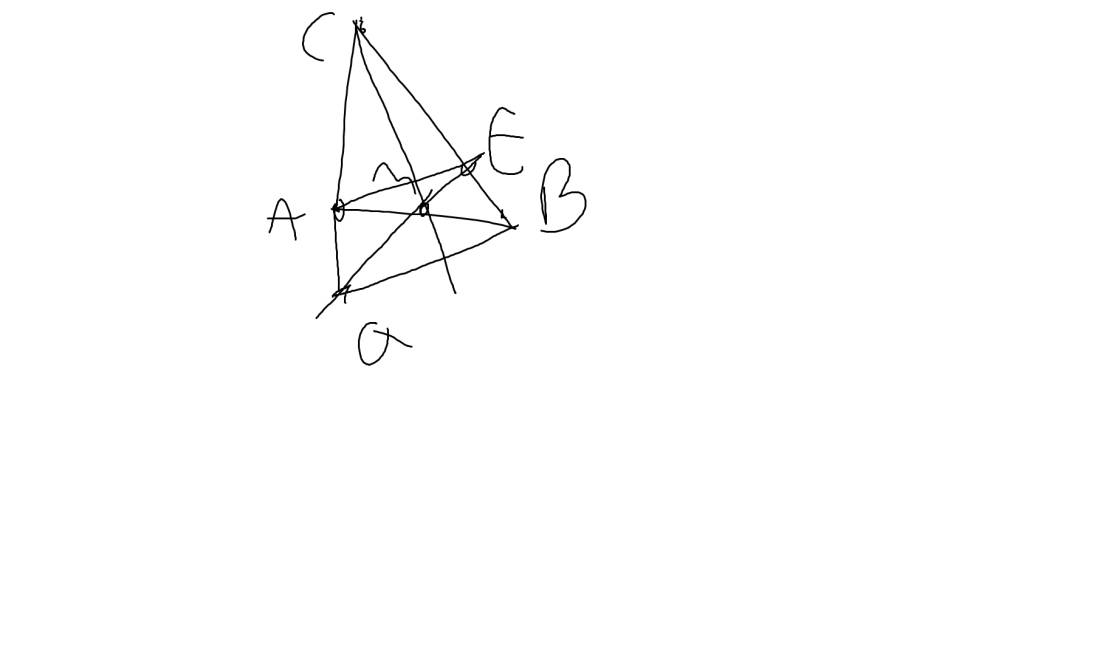
b: Xét ΔMBC và ΔMED có
\(\widehat{MCB}=\widehat{MDE}\)(BC//DE)
MC=MD
\(\widehat{BMC}=\widehat{EMD}\)(hai góc đối đỉnh)
Do đó: ΔMBC=ΔMED
=>BC=ED
Xét ΔDEB có DE+DB>BE
mà DE=BC
nên BC+BD>BE
c:
ΔMBC=ΔMED
=>ME=MB
=>M là trung điểm của EB
Ta có: AD=AB
mà A nằm giữa B và D
nên A là trung điểm của BD
Xét ΔCDB có
CA là đường trung tuyến
CA là đường cao
Do đó: ΔCDB cân tại C
=>CD=CB
Xét ΔEDB có
DM,EA là các đường trung tuyến
DM cắt EA tại G
Do đó: G là trọng tâm của ΔEDB
=>DM=3GM
mà DM=1/2DC
nên 3GM=1/2DC
=>DC=6GM
=>BC=6GM

a: ΔABC vuông tại A
=>\(\widehat{ABC}+\widehat{ACB}=90^0\)
=>\(\widehat{ACB}=40^0\)
Xét ΔABC có \(\widehat{ABC}>\widehat{ACB}\)
mà AC,AB lần lượt là cạnh đối diện của các góc ABC,ACB
nên AC>AB
b: Xét ΔCAM và ΔCEM có
CA=CE
\(\widehat{ACM}=\widehat{ECM}\)
CM chung
Do đó: ΔCAM=ΔCEM
c: Ta có: ΔCAM=ΔCEM
=>MA=ME
=>M nằm trên đường trung trực của AE(1)
ta có: CA=CE
=>C nằm trên đường trung trực của AE(2)
Từ (1),(2) suy ra CM là đường trung trực của AE
=>CM\(\perp\)AE tại trung điểm của AE
Xét ΔMAE có MA=ME
nên ΔMAE cân tại M
=>\(\widehat{MAE}=\widehat{MEA}\)
d: Xét ΔCEQ vuông tại E và ΔCAB vuông tại A có
CE=CA
\(\widehat{ECQ}\) chung
Do đó: ΔCEQ=ΔCAB
=>CQ=CB
Xét ΔCQB có \(\dfrac{CA}{CQ}=\dfrac{CE}{CB}\)
nên AE//QB

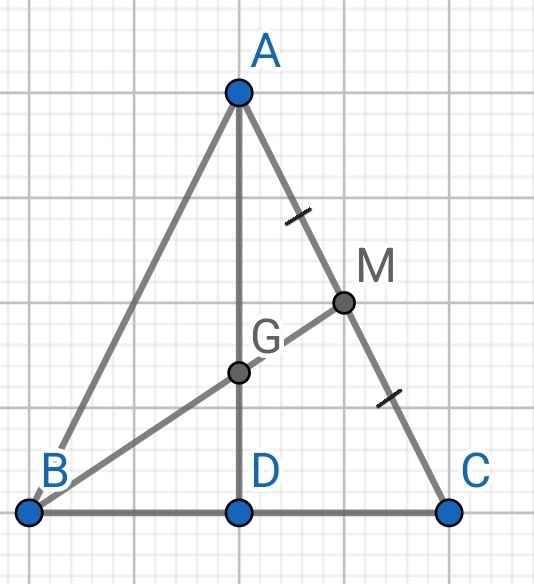
∆ABC cân tại A (gt)
AD là đường phân giác (gt)
⇒ AD cũng là đường trung tuyến của ∆ABC
Lại có BM là đường trung tuyến thứ hai của ∆ABC (gt)
Mà BM cắt AD tại G (gt)
⇒ G là trọng tâm của ABC
⇒ AG = 2GD


a: A(x)+B(x)
\(=x^3-3x^2+3x-1+2x^3+x^2-x+5\)
\(=3x^3-2x^2+2x+4\)
b: A(x)*C(x)
\(=\left(x^3-3x^2+3x-1\right)\left(x-2\right)\)
\(=x^4-2x^3-3x^3+6x^2+3x^2-6x-x+2\)
\(=x^4-5x^3+9x^2-7x+2\)

a) \(\dfrac{5}{3}=\dfrac{x}{9}\)
\(\Rightarrow x=\dfrac{5}{3}\cdot9\)
\(\Rightarrow x=15\)
Vậy x = 15.
b) Gọi số sách của hai lớp 7A và 7B lần lượt là \(a\), \(b\) (sách; \(a,b\in\mathbb{N}^*\))
Vì số sách của hai lớp 7A và 7B tỉ lệ thuận với số học sinh của mỗi lớp, mà số học sinh hai lớp lần lượt là 32 và 36 nên: \(\dfrac{a}{32}=\dfrac{b}{36}\)
Vì lớp 7A quyên góp được ít hơn lớp 7B 8 quyển sách nên: \(b-a=8\) (1)
Áp dụng tính chất của dãy tỉ số bằng nhau và (1), ta được:
\(\dfrac{a}{32}=\dfrac{b}{36}=\dfrac{b-a}{36-32}=\dfrac{8}{4}=2\)
\(\Rightarrow\left\{{}\begin{matrix}a=2\cdot32=64\left(tm\right)\\b=2\cdot36=72\left(tm\right)\end{matrix}\right.\)
Vậy lớp 7A và lớp 7B quyên góp được số sách lần lượt là 64 quyển sách và 72 quyển sách.
\(Toru\)

a: Xét ΔMAB và ΔMEC có
MA=ME
\(\widehat{AMB}=\widehat{EMC}\)(hai góc đối đỉnh)
MB=MC
Do đó: ΔMAB=ΔMEC
=>\(\widehat{MAB}=\widehat{MEC}\)
mà hai góc này là hai góc ở vị trí so le trong
nên AB//CE

ΔABC cân tại A
mà AD là đường trung tuyến
nên AD\(\perp\)BC
ΔADB vuông tại D
=>\(DA^2+DB^2=AB^2\)
ΔADB vuông tại D có DE là đường cao
nên \(S_{ADB}=\dfrac{1}{2}\cdot DA\cdot DB=\dfrac{1}{2}\cdot DE\cdot AB\)
=>\(DA\cdot DB=DE\cdot AB\)
\(\left(DE+AB\right)^2-\left(DA+DB\right)^2\)
\(=DE^2+AB^2+2\cdot DE\cdot AB-DA^2-DB^2-2\cdot DA\cdot DB\)
\(=DE^2+AB^2-AD^2-BD^2+2\cdot DE\cdot AB-2\cdot DE\cdot AB\)
\(=DE^2>0\)
=>\(\left(DE+AB\right)^2>\left(DA+DB\right)^2\)
=>DE+AB>DA+DB


a: Thể tích của bể nước là:
\(2\cdot1,5\cdot1,2=3,6\left(m^3\right)=3600\left(lít\right)\)
b: thể tích nước đã chảy vào bể là:
4x600=2400(lít)=2,4m3
Chiều cao của mực nước là:
2,4:2:1,5=1,2:1,5=0,8(m)