Tính hợp lí: –5/8×2/19–5/8×17/19
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


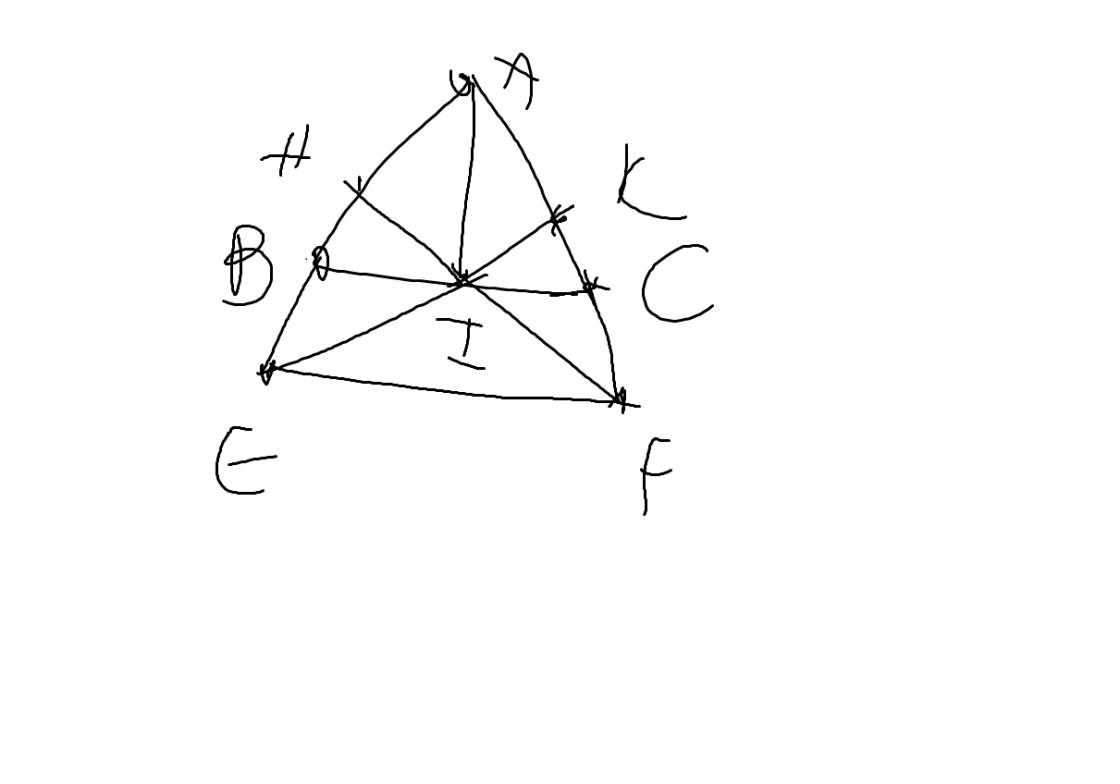
a: Xét ΔIHB vuông tại H và ΔIKC vuông tại K có
IB=IC
\(\widehat{B}=\widehat{C}\)
Do đó: ΔIHB=ΔIKC
b: Ta có: ΔIHB=ΔIKC
=>IB=IC
mà IC>IK(ΔIKC vuông tại K)
nên IB>IK
c:
Ta có: ΔIHB=ΔIKC
=>IH=IK
Xét ΔHIE vuông tại H và ΔKIF vuông tại K có
IH=IK
\(\widehat{HIE}=\widehat{KIF}\)(hai góc đối đỉnh)
Do đó; ΔHIE=ΔKIF
=>HE=KF
Ta có: AH+HB=AB
AK+KC=AC
mà HB=KC và AB=AC
nên AH=AK
Ta có: AH+HE=AE
AK+KF=AF
mà AH=AK và HE=KF
nên AE=AF
=>ΔAEF cân tại A
d: Xét ΔAEF có \(\dfrac{AH}{AE}=\dfrac{AK}{AF}\)
nên HK//EF
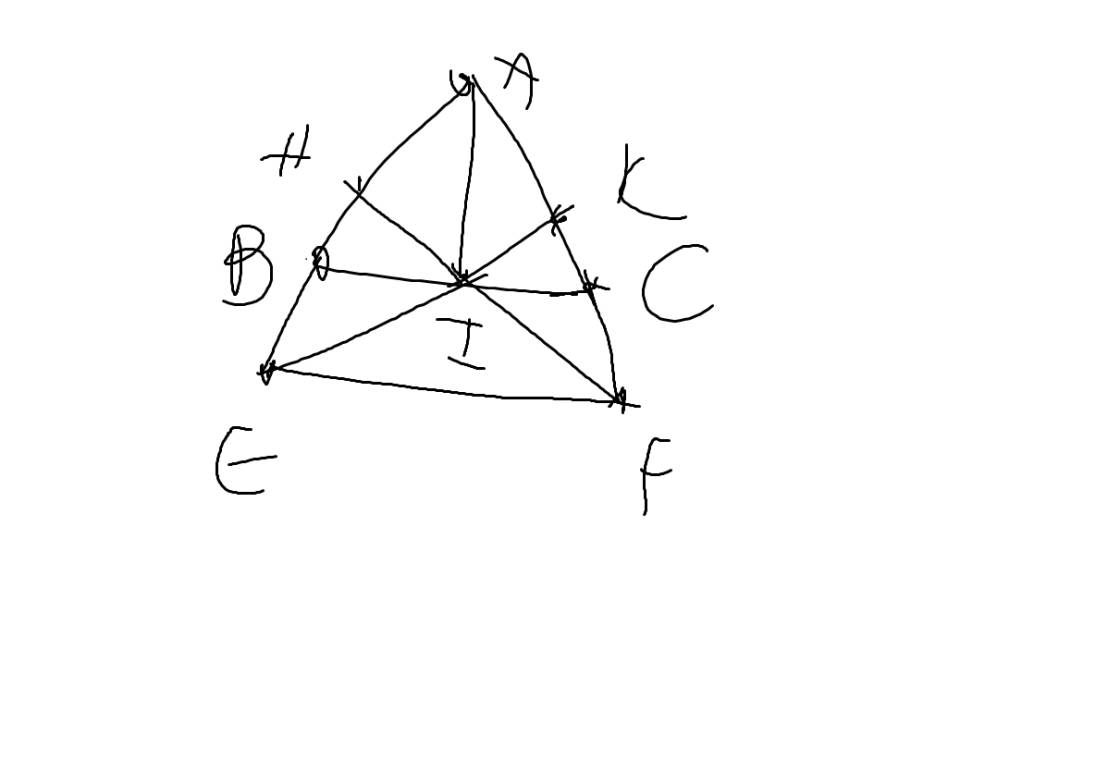

a: Xét ΔIHB vuông tại H và ΔIKC vuông tại K có
IB=IC
\(\widehat{B}=\widehat{C}\)
Do đó: ΔIHB=ΔIKC
b: Ta có: ΔIHB=ΔIKC
=>IB=IC
mà IC>IK(ΔIKC vuông tại K)
nên IB>IK
c:
Ta có: ΔIHB=ΔIKC
=>IH=IK
Xét ΔHIE vuông tại H và ΔKIF vuông tại K có
IH=IK
\(\widehat{HIE}=\widehat{KIF}\)(hai góc đối đỉnh)
Do đó; ΔHIE=ΔKIF
=>HE=KF
Ta có: AH+HB=AB
AK+KC=AC
mà HB=KC và AB=AC
nên AH=AK
Ta có: AH+HE=AE
AK+KF=AF
mà AH=AK và HE=KF
nên AE=AF
=>ΔAEF cân tại A
d: Xét ΔAEF có \(\dfrac{AH}{AE}=\dfrac{AK}{AF}\)
nên HK//EF

Số gà trống so với số gà mái là:
\(\dfrac{15}{80}=\dfrac{3}{16}\)

Tổng số gà có trong trang trại là:
\(15+80=95\) (con)
Phân số biểu thị số gà trống so với số gà của trang trại là:
\(\dfrac{15}{95}=\dfrac{15:5}{95:5}=\dfrac{3}{19}\)

a) Số cây cam trong vườn là:
$\frac{9}{25} \times 250 = 90$ (cây)
Số cây táo trong vườn là:
$\frac{1}{5} \times 250 = 50$ (cây)
Số cây ổi trong vườn là:
$250 - 90 - 50 = 110$ (cây)
b) Tỉ lệ cây cam:
$\frac{90}{250} \times 100\% = 36\%$
Tỉ lệ cây táo:
$\frac{50}{250} \times 100\% = 20\%$
Tỉ lệ cây ổi:
$\frac{110}{250} \times 100\% = 44\%$
Đáp số: a) 110 cây ổi
b) 36% cây cam
20% cây táo
44% cây ổi
a) Số cây cam có trong vườn là:
\(\dfrac{9}{25}\times250=90\) (cây)
Số cây táo có trong vườn là:
\(\dfrac{1}{5}\times250=50\) (cây)
Số cây ổi có trong vườn là:
\(250-50-90=110\) (cây)
b) Tỉ số phần trăm mỗi loại cây trong vườn là:
Số cây cam: \(\dfrac{90}{250}\times100\%=36\%\)
Số cây táo: \(\dfrac{50}{250}\times100\%=20\%\)
Số cây ổi: \(100\%-36\%-20\%=44\%\)

\(xy-2y+x=3\)
\(\Rightarrow y\left(x-2\right)+x=3\)
\(\Rightarrow y\left(x-2\right)+\left(x-2\right)=3-2\)
\(\Rightarrow\left(x-2\right)\left(y+1\right)=1\)
Do x và y là các số tự nhiên nên ta có bảng:
| x - 2 | 1 | -1 |
| y + 1 | 1 | -1 |
| x | 3 | 1 |
| y | 0 | -2 |
Mà: `x,y∈N`
`⇒(x;y)=(3;1)`

\(\left(x+15\right):\dfrac{3}{4}=2x-30\)
\(\Leftrightarrow\left(x+15\right)\cdot\dfrac{4}{3}=2x-30\)
\(\Leftrightarrow\dfrac{4}{3}x+20=2x-30\)
\(\Leftrightarrow2x-\dfrac{4}{3}x=20+30\)
\(\Leftrightarrow\dfrac{2}{3}x=50\)
\(\Leftrightarrow x=50\cdot\dfrac{3}{2}\)
\(\Leftrightarrow x=75\)
Vậy: ...

Hệ số góc của đường thẳng (d1) là m - 2.
Hệ số góc của đường thẳng (d2) là 3.
Vì vậy, để hai đường thẳng (d1) và (d2) song song nhau, ta cần có:
m - 2 = 3
=> m = 3 + 2
=> m = 5
Vậy, giá trị m cần tìm là m = 5.
ĐK: `m≠2`
Ta có:
(d1) \(y=\left(m-2\right)x+4\left(a_1=m-2;b_1=4\right)\)
(d2) \(y=3x-1\left(a_2=3;b_2=-1\right)\)
Để (d1) và (d2) song song với nhau thì:
\(\left\{{}\begin{matrix}a_1=a_2\\b_1\ne b_2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m-2=3\\4\ne-1\end{matrix}\right.\)
\(\Leftrightarrow m=5\left(tm\right)\)
\(-\dfrac{5}{8}\times\dfrac{2}{19}-\dfrac{5}{8}\times\dfrac{17}{19}\\ =-\dfrac{5}{8}\times\left(\dfrac{2}{19}+\dfrac{17}{19}\right)\\ =-\dfrac{5}{8}\times1\\ =-\dfrac{5}{8}.\)