Tìm giá trị của biểu thức A(x) tại x = 2023 với A(x) = x5 - 2024x4 + 2024x3 - 2024x2 +2024x - 2024
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(P\left(x\right)=x^{2023}-2022x^{2022}-2022x^{2021}-\dots-2022x^2-2022x+1\)
\(\Rightarrow P\left(2023\right)=2023^{2023}-2022\cdot2023^{2022}-2022\cdot2023^{2021}-\dots-2022\cdot2023^2-2022\cdot2023+1\)
\(=2023^{2023}-\left(2023-1\right)\cdot2023^{2022}-\left(2023-1\right)\cdot2023^{2021}-\dots-\left(2023-1\right)\cdot2023^2-\left(2023-1\right)\cdot2023+1\)
\(=2023^{2023}-2023^{2023}+2023^{2022}-2023^{2022}+2023^{2021}-\dots-2023^3+2023^2-2023^2+2023+1\)
\(=2024\)
___
Cách giải: Tách các hệ số để làm xuất hiện các lũy thừa của \(2023\)
Ta thấy: \(x=2023\Rightarrow x-1=2022\)
Ta có:
\(P\left(x\right)=x^{2023}-\left(x-1\right)\times x^{2022}-\left(x-1\right)\times x^{2021}-...-\left(x-1\right)\times x^2-\left(x-1\right)\times x+1\)\(P\left(x\right)=x^{2023}-x^{2023}+x^{2022}-x^{2022}+x^{2021}-....-x^3+x^2-x^2+x+1\)
\(P\left(x\right)=x+1\)
Thay x=2023, ta có:
\(P\left(2023\right)=2023+1=2024\)

x=2023 nên x-1=2022
\(P=x^{2023}-2022x^{2022}-2021x^{2021}-...-2022x+1\)
\(=x^{2023}-x^{2022}\left(x-1\right)-x^{2021}\left(x-1\right)-...-x\left(x-1\right)+1\)
\(=x^{2023}-x^{2023}+x^{2022}-x^{2022}+...-x^2+x+1\)
=x+1
=2023+1=2024

a: Xét ΔABD vuông tại A và ΔEBD vuông tại E có
BD chung
\(\widehat{ABD}=\widehat{EBD}\)
Do đó: ΔABD=ΔEBD
b: ΔABD=ΔEBD
=>BA=BE
Xét ΔBEF vuông tại E và ΔBAC vuông tại A có
BE=BA
\(\widehat{EBF}\) chung
Do đó: ΔBEF=ΔBAC
=>BF=BC
c: Xét ΔBFC có \(\dfrac{BA}{BF}=\dfrac{BE}{BC}\)
nên AE//FC
Ta có: AE//FC
AH\(\perp\)FC
Do đó: AE\(\perp\)AH

a: Xét ΔABM và ΔCDM có
MA=MC
\(\widehat{AMB}=\widehat{CMD}\)(hai góc đối đỉnh)
MB=MD
Do đó; ΔABM=ΔCDM
b: Xét ΔCBD có
CM,DN là các đường trung tuyến
CM cắt DN tại G
Do đó: G là trọng tâm của ΔCBD
c: \(2\left(BM-BN\right)=2\cdot BM-2\cdot BN=BD-BC\)
mà BD-BC<CD(Hệ quả BĐT tam giác trong ΔBCD)
và CD=AB
nên 2(BM-BN)<AB
=>\(BM-BN< \dfrac{AB}{2}\)


2:
a: \(\left(x+3\right)\left(x^2+3x-5\right)\)
\(=x^3+3x^2-5x+3x^2+9x-15\)
\(=x^3+6x^2+4x-15\)
b: \(\left(3x^3-4x^2+6x\right):3x\)
\(=3x^3:3x-4x^2:3x+6x:3x\)
\(=x^2-\dfrac{4}{3}x+2\)
Bài 1:
a: \(A=15-2x^2+3x^2-3x-15\)
\(=\left(-2x^2+3x^2\right)-3x+\left(15-15\right)\)
\(=x^2-3x\)
Khi x=8 thì \(A=8^2-3\cdot8=64-24=40\)
b: Đặt A=0
=>x(x-3)=0
=>\(\left[{}\begin{matrix}x=0\\x=3\end{matrix}\right.\)

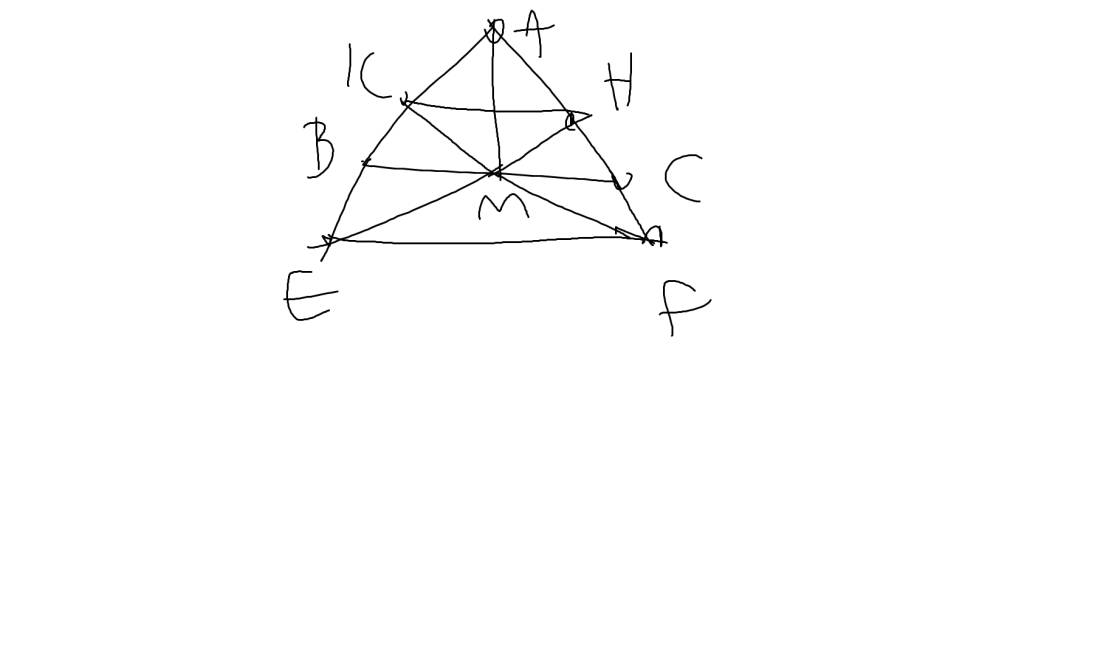
a: Xét ΔAMB và ΔAMC có
AM chung
MB=MC
AB=AC
Do đó: ΔAMB=ΔAMC
=>\(\widehat{BAM}=\widehat{CAM}\)
=>AM là phân giác của góc BAC
b: Xét ΔAKM vuông tại K và ΔAHM vuông tại H có
AM chung
\(\widehat{KAM}=\widehat{HAM}\)
Do đó: ΔAKM=ΔAHM
=>MK=MH
mà MH<MF(ΔMHF vuông tại H)
nên MK<MF
c: Xét ΔMKE vuông tại K và ΔMHF vuông tại H có
MK=MH
\(\widehat{KME}=\widehat{HMF}\)(hai góc đối đỉnh)
Do đó: ΔMKE=ΔMHF
=>KE=HF
Xét ΔAEF có \(\dfrac{AK}{KE}=\dfrac{AH}{HF}\)
nên KH//EF

Biến cố ngẫu nhiên là A,D
Biến cố chắc chắn là C
Biến cố không thể là B


x=2023 nên x+1=2024
\(A\left(x\right)=x^5-2024x^4+2024x^3-2024x^2+2024x-2024\)
\(=x^5-x^4\left(x+1\right)+x^3\left(x+1\right)-x^2\left(x+1\right)+x\left(x+1\right)-\left(x+1\right)\)
\(=x^5-x^5-x^4+x^4+...-x-1\)
=-1