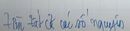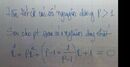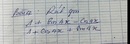\(\hept{\begin{cases}x+3y+2z=-1\left(1\right)\\4y+3x=1,5\left(2\right)\\2z=3\left(3\right)\end{cases}}\)

\(\left(3\right)\Rightarrow z=\frac{3}{2}\)Thay vào pt (1) ta được: 

hệ phương trình có dạng \(\hept{\begin{cases}x+3y+3=-1\\4y+3x=1,5\end{cases}}\)

\(\Leftrightarrow\hept{\begin{cases}x+3y=-4\\3x+4y=1,5\end{cases}\Leftrightarrow\hept{\begin{cases}3x+9y=-12\\3x+4y=1,5\end{cases}}}\)

\(\Leftrightarrow\hept{\begin{cases}5y=-\frac{27}{2}\\x+3y=-4\end{cases}\Leftrightarrow\hept{\begin{cases}y=-\frac{27}{10}\\x=-4-3.\left(-\frac{27}{10}\right)=\frac{41}{10}\end{cases}}}\)

Vậy hệ pt có một nghiệm ( x ; y ; z ) = ( \(\frac{41}{10};-\frac{27}{10};\frac{3}{2}\))

Ta có 2z = 3 

=> z = 1,5

Khi đó x + 3y + 2z = -1

<=> x + 3y + 3 = -1

<=> x + 3y = -4

<=> 3x + 9y = -12

<=> 3x + 4y + 5y = -12

<=> 1,5 + 5y = -12

<=> y = -2,7

=> x = [1,5 - 4.(-2,7)]  : 3 = 4,1

Vậy x = 4,1 ; y = -2,7 ; z = 1,5 

\(\cos\left(\frac{\pi}{6}\left(4x+\sqrt{10+x^2}\right)\right)=-\frac{\sqrt{3}}{2}\)

\(\cos\left(\frac{\pi}{6}\left(4x+\sqrt{10+x^2}\right)\right)=\cos\left(\frac{5\pi}{6}\right)\)

\(\frac{\pi}{6}\left(4x+\sqrt{10+x^2}\right)=\frac{5\pi}{6}\)

\(4x+\sqrt{10+x^2}=5\)

\(\sqrt{10+x^2}=5-4x\)

\(10+x^2=25-40x+16x^2\)

\(15-40x+15x^2=0\)

\(\sqrt{\Delta}=10\sqrt{7}\)

\(\orbr{\begin{cases}x_1=\frac{40+10\sqrt{7}}{30}=\frac{4+\sqrt{7}}{3}\left(ktm\right)\\x_2=\frac{40-10\sqrt{7}}{30}=\frac{4-\sqrt{7}}{3}\left(tm\right)\end{cases}}\)

vậy pt có n⁰ duy nhất là \(\frac{4-\sqrt{7}}{3}\)

????????????? nhs riêng cho thầy cô chứ 

Cái này phải hỏi riêng Thầy, Cô chứ sao lại đăng lên đây

\(x^3+px^2+\left(p-1+\frac{1}{p-1}\right)x+1=0\)

\(\Leftrightarrow\left[x-\left(1-p\right)\right]\left[\left(p-1\right)x^2+\left(p-1\right)x+1\right]=0\)

\(\Leftrightarrow\orbr{\begin{cases}x=1-p\\\left(p-1\right)x^2+\left(p-1\right)x+1=0\end{cases}}\left(1\right)\)

Để pt có no duy nhất <=> hệ pt (1) có no duy nhất

<=> pt(1) vô no hoặc pt(1) có nghiệm kép x₁=x₂=1-p

Kết hợp điều kiện \(p>1,p\inℕ\)ta tìm được các giá trị của p thỏa mãn là

p=2,3,4

\(x^3+px^2+\left(p-1+\frac{1}{p-1}\right)x+1=0\)

\(\Leftrightarrow\left(p-1\right)x^3+p\left(p-1\right)x^2+\left(p^2-2p+2\right)x+p-1=0\)

\(\Leftrightarrow\left(x+p-1\right)\left[x^2\left(p-1\right)+x\left(p-1\right)+1\right]=0\)

\(\Leftrightarrow\orbr{\begin{cases}x=1-p\\x^2\left(p-1\right)+x\left(p-1\right)+1=0\left(1\right)\end{cases}}\)

Phương trình có nghiệm duy nhất khi phương trình \(\left(1\right)\)vô nghiệm hoặc có nghiệm kép bằng \(1-p\). 

- \(\left(1\right)\)vô nghiệm: 

\(\Delta< 0\Leftrightarrow\left(p-1\right)^2-4\left(p-1\right)< 0\Leftrightarrow1< p< 5\).

- \(\left(1\right)\)có nghiệm kép bằng \(1-p\).

\(\left(1\right)\)có nghiệm bằng \(1-p\)suy ra \(\left(1-p\right)^2\left(p-1\right)+\left(1-p\right)\left(p-1\right)+1=0\)

mà \(p>1\)nên phương trình này vô nghiệm. 

Vậy \(1< p< 5\)mà \(p\)nguyên nên \(p\in\left\{2;3;4\right\}\).

\(A=\frac{1+sin4x-cos4x}{1+sin4x+cos4x}=\frac{sin4x+\left(1-cos4x\right)}{sin4x+\left(1+cos4x\right)}=\frac{sin4x+2sin^22x}{sin4x+2cos^22x}=\frac{2sin2x\left(cos2x+sin2x\right)}{2cos2x\left(sin2x+cos2x\right)}\)

\(=\frac{2sin2x}{2cos2x}=tan2x\)