tính giá trị biểu thức (2a-b)/(3a-b) +(5b-a)/(3a+ b) biết 3a^3-6a^2b +ab^2-2b^3=0 và 9a^2-b^2 khác 0
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


ΔBAC vuông cân tại A nên AB=AC=5cm
ΔABC vuông tại A
=>\(BC^2=AB^2+AC^2\)
=>\(BC=\sqrt{5^2+5^2}=5\sqrt{2}\left(cm\right)\)
ΔBAC vuông cân tại A nên AB=AC=5cm
BC là cạnh huyền
Áp dụng định lý Pytago ta có :
BC2= AB2+ AC2
BC2 = 25+25=50
BC = 5 \(\sqrt{ }\)2(cm)

a: Số tiền tiết kiệm được trong tháng 3 là x+y(đồng)
Số tiền tiết kiệm được trong tháng 4 là y+x+y=x+2y(đồng)
Số tiền tiết kiệm được trong tháng 5 là:
x+y+x+2y=2x+3y(đồng)
b: Số tiền tiết kiệm được trong tháng 6 là:
x+2y+2x+3y=3x+5y(đồng)
Số tiền tiết kiệm trong tháng 2 nhiều hơn trong tháng giêng là 20000 đồng nên y=x+20000
=>Số tiền tiết kiệm được trong tháng 6 là:
3x+5(x+20000)=8x+100000(đồng)
Theo đề, ta có:
8x+100000=340000
=>8x=240000
=>x=30000
=>y=30000+20000=50000(đồng)
Số tiền của đôi giày là:
x+y+x+y+x+2y+2x+3y+3x+5y
=8x+12y
\(=8\cdot30000+12\cdot50000=840000\left(đồng\right)\)
@Nguyễn Lê Phước Thịnh: làm bạn sao hay vậy?

Lời giải:
$A=\frac{8x-2}{x^2+3}$
$\Rightarrow A(x^2+3)=8x-2$
$\Leftrightarrow Ax^2-8x+(3A+2)=0(*)$
Xét $A\neq 0$. Vì $A$ tồn tại nên PT $(*)$ tồn tại, nghĩa là $(*)$ có nghiệm
$\Leftrightarrow \Delta'=16-A(3A+2)\geq 0$
$\Leftrightarrow 3A^2+2A-16\leq 0$
$\Leftrightarrow (A-2)(3A+8)\leq 0$
$\Leftrightarrow \frac{-8}{3}\leq A\leq 2$
Vậy $A_{\max}=2$

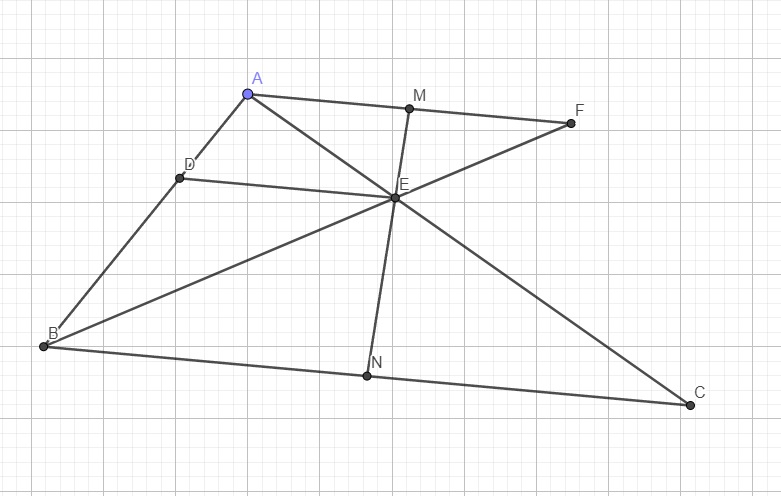
Do M là trung điểm AF \(\Rightarrow AM=\dfrac{1}{2}AF=\dfrac{9}{2}\left(cm\right)\)
\(CE=AC-AE=10\left(cm\right)\)
Theo giả thiết, AF song song BC nên AM song song CN, áp dụng định lý talet:
\(\dfrac{AM}{CN}=\dfrac{AE}{CE}\) \(\Rightarrow CN=\dfrac{AM.CE}{AE}=\dfrac{\dfrac{9}{2}.10}{5}=9\left(cm\right)\)
Mà \(BC=18\left(cm\right)\Rightarrow CN=\dfrac{1}{2}BC\)
\(\Rightarrow N\) là trung điểm của BC

a: Ta có: ΔABC vuông tại A
=>\(AB^2+AC^2=BC^2\)
=>\(AC^2=5^2-3^2=16=4^2\)
=>AC=4(cm)
Xét ΔBAC có
M,N lần lượt là trung điểm của BA,BC
=>MN là đường trung bình của ΔBAC
=>MN//AC và \(MN=\dfrac{1}{2}AC=\dfrac{1}{2}\cdot4=2\left(cm\right)\)
b: Xét tứ giác AMNC có MN//AC
nên AMNC là hình thang
Hình thang AMNC có \(\widehat{MAC}=90^0\)
nên AMNC là hình thang vuông
c: Ta có: ΔABC vuông tại A
mà AN là đường trung tuyến
nên BC=2AN
Xét ΔBAC có BD là phân giác
nên \(\dfrac{DA}{DC}=\dfrac{BA}{BC}\)
=>\(\dfrac{DA}{DC}=\dfrac{2\cdot AM}{2\cdot AN}=\dfrac{AM}{AN}\)

Gọi thời gian xưởng làm theo kế hoạch là x (ngày) với x>3
Số áo xưởng phải dệt theo kế hoạch là: \(30x\) (áo)
Số ngày thực tế là: \(x-3\) (ngày)
Số áo thực tế dệt được là: \(40\left(x-3\right)\) (áo)
Do xưởng làm thêm được 20 chiếc áo nữa nên ta có pt:
\(40\left(x-3\right)-30x=20\)
\(\Leftrightarrow10x-120=20\)
\(\Leftrightarrow10x=140\)
\(\Leftrightarrow x=14\)

a. Em tự giải
b.
Ta có: \(\widehat{CAH}=\widehat{ABC}\) (cùng phụ \(\widehat{ACB}\))
Mà \(\widehat{FAE}=\dfrac{1}{2}\widehat{CAH}\) (do AD là phân giác)
\(\widehat{HBE}=\dfrac{1}{2}\widehat{ABC}\) (do BK là phân giác)
\(\Rightarrow\widehat{FAE}=\widehat{HBE}\)
Xét hai tam giác AEF và BEH có:
\(\left\{{}\begin{matrix}\widehat{FAE}=\widehat{HBE}\left(cmt\right)\\\widehat{AEF}=\widehat{BEH}\left(\text{đối đỉnh}\right)\end{matrix}\right.\)
\(\Rightarrow\Delta AEF\sim\Delta BEH\left(g.g\right)\)
\(\Rightarrow\dfrac{EA}{EB}=\dfrac{EF}{EH}\Rightarrow EA.EH=EF.EB\)
c.
Do \(\Delta AEF\sim\Delta BEH\Rightarrow\widehat{AFE}=\widehat{BHE}=90^0\)
\(\Rightarrow BF\perp AD\) tại F
Trong tam giác ABD, BF vừa là đường cao vừa là phân giác nên \(\Delta ABD\) cân tại B
\(\Rightarrow BF\) là trung trực AD hay \(BK\) là trung trực của AD
\(\Rightarrow KA=KD\Rightarrow\Delta ADK\) cân tại K
\(\Rightarrow\widehat{KDA}=\widehat{KAD}\)
Mà \(\widehat{KAD}=\widehat{DAH}\) (do AD là phân giác)
\(\Rightarrow\widehat{KDA}=\widehat{DAH}\Rightarrow KD||AH\) (hai góc so le trong bằng nhau)
d.
Xét hai tam giác ABC và HBA có:
\(\left\{{}\begin{matrix}\widehat{B}-chung\\\widehat{BAC}=\widehat{BHA}=90^0\end{matrix}\right.\)
\(\Rightarrow\Delta ABC\sim\Delta HBA\left(g.g\right)\Rightarrow\dfrac{AB}{BH}=\dfrac{BC}{AB}\Rightarrow\dfrac{AB}{BC}=\dfrac{BH}{AB}\) (1)
Theo cm câu c, do \(\Delta ABD\) cân tại B \(\Rightarrow AB=BD\) (2)
(1);(2) \(\Rightarrow\dfrac{AB}{BC}=\dfrac{BH}{BD}\)
Cũng theo câu c, do \(KD||AH\), áp dụng định lý Talet trong tam giác BKD:
\(\dfrac{BH}{BD}=\dfrac{EH}{KD}\)
\(\Rightarrow\dfrac{AB}{BC}=\dfrac{EH}{KD}\)
\(\Rightarrow\dfrac{EH}{AB}=\dfrac{KD}{BC}\)

a: Xét ΔABD vuông tại Dvà ΔACE vuông tại E có
\(\widehat{BAD}\) chung
Do đó: ΔABD~ΔACE
b: Ta có: ΔABD~ΔACE
=>\(\dfrac{AB}{AC}=\dfrac{AD}{AE}\)
=>\(\dfrac{2}{AE}=\dfrac{4}{5}\)
=>\(AE=2\cdot\dfrac{5}{4}=2\cdot1,25=2,5\left(cm\right)\)
c: Xét tứ giác BEDC có \(\widehat{BEC}=\widehat{BDC}=90^0\)
nên BEDC là tứ giác nội tiếp
=>\(\widehat{EDH}=\widehat{BCH}\)



Đặt \(B=\dfrac{2a-b}{3a-b}+\dfrac{5b-a}{3a+b}\)
ĐKXĐ: \(b\ne\pm3a\)
\(3a^3-6a^2b+ab^2-2b^3=0\)
=>\(3a^2\left(a-2b\right)+b^2\left(a-2b\right)=0\)
=>\(\left(a-2b\right)\left(3a^2+b^2\right)=0\)
=>\(\left\{{}\begin{matrix}a=2b\left(nhận\right)\\a=b=0\left(loại\right)\end{matrix}\right.\)
Thay a=2b vào B, ta được:
\(B=\dfrac{2\cdot2b-b}{3\cdot2b-b}+\dfrac{5b-2b}{3\cdot2b+b}=\dfrac{4-1}{6-1}+\dfrac{5-2}{6+1}\)
\(=\dfrac{3}{5}+\dfrac{3}{7}=\dfrac{3\cdot7+3\cdot5}{35}=\dfrac{36}{35}\)