Chiều cao của mỗi hình chóp tứ giác đều là:

     30:2=1530:2=15 (m).

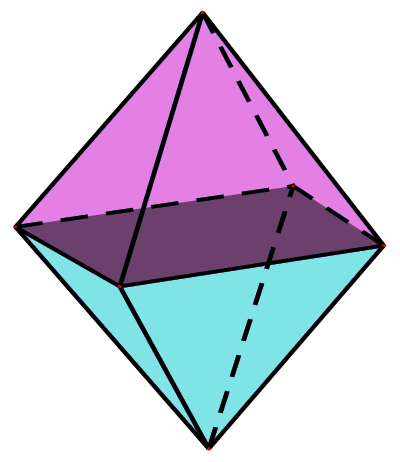
Thể tích của lồng đèn quả trám là:

     𝑉=2.(13.20.20.15)=4000V=2.(31​.20.20.15)=4000 (cm33).

a) Xét hai tam giác vuông: \(\Delta BHK\) và \(\Delta CHI\) có:

\(\widehat{BHK}=\widehat{CHI}\) (đối đỉnh)

\(\Rightarrow\Delta BHK\) ∽ \(\Delta CHI\left(g-g\right)\)

b) Do \(BH\) là tia phân giác của \(\widehat{KBC}\) (gt)

\(\Rightarrow\widehat{KBH}=\widehat{CBH}\)

\(\Rightarrow\widehat{KBH}=\widehat{CBI}\) (1)

Do \(\Delta BHK\) ∽ \(\Delta CHI\left(cmt\right)\)

\(\Rightarrow\widehat{KBH}=\widehat{ICH}\) (2)

Từ (1) và (2) \(\Rightarrow\widehat{ICH}=\widehat{CBI}\)

Xét hai tam giác vuông: \(\Delta CIB\) và \(\Delta HIC\) có:

\(\widehat{CBI}=\widehat{ICH}\left(cmt\right)\)

\(\Rightarrow\Delta CIB\) ∽ \(\Delta HIC\left(g-g\right)\)

\(\Rightarrow\dfrac{CI}{IH}=\dfrac{IB}{CI}\)

\(\Rightarrow CI^2=IH.IB\)

c) Do \(CI\perp BH\) tại \(I\) (gt)

\(\Rightarrow BI\perp AC\)

\(\Rightarrow BI\) là đường cao của \(\Delta ABC\)

Lại có:

\(CK\perp KB\left(gt\right)\)

\(\Rightarrow CK\perp AB\)

\(\Rightarrow CK\) là đường cao thứ hai của \(\Delta ABC\)

Mà H là giao điểm của \(BI\) và \(CK\) (gt)

\(\Rightarrow AH\) là đường cao thứ ba của \(\Delta ABC\)

\(\Rightarrow AD\perp BC\)

Xét hai tam giác vuông: \(\Delta BKH\) và \(\Delta BDH\) có:

\(BH\) là cạnh chung

\(\widehat{KBH}=\widehat{DBH}\) (do BH là tia phân giác của \(\widehat{B}\))

\(\Rightarrow\Delta BKH=\Delta BDH\) (cạnh huyền - góc nhọn)

\(\Rightarrow BK=BD\) (hai cạnh tương ứng)

\(\Rightarrow B\) nằm trên đường trung trực của DK (3)

Do \(\Delta BKH=\Delta BDH\left(cmt\right)\)

\(\Rightarrow HK=HD\) (hai cạnh tương ứng)

\(\Rightarrow H\) nằm trên đường trung trực của DK (4)

Từ (3) và (4) \(\Rightarrow BH\) là đường trung trực của DK

\(\Rightarrow\widehat{DKH}+\widehat{BHK}=90^0\)

Mà \(\widehat{BHK}=\widehat{CHI}\) (cmt)

\(\Rightarrow\widehat{DKH}+\widehat{CHI}=90^0\) (*)

\(\Delta ABC\) có:

\(BH\) là đường phân giác (cmt)

\(BH\) cũng là đường cao (cmt)

\(\Rightarrow\Delta ABC\) cân tại B

\(\Rightarrow BH\) là đường trung trực của \(\Delta ABC\)

\(\Rightarrow I\) là trung điểm của AC

\(\Rightarrow KI\) là đường trung tuyến của \(\Delta AKC\)

\(\Delta AKC\) vuông tại K có KI là đường trung tuyến ứng với cạnh huyền AC

\(\Rightarrow KI=IC=IA=\dfrac{AC}{2}\)

\(\Rightarrow\Delta IKC\) cân tại \(I\)

\(\Rightarrow\widehat{IKC}=\widehat{ICK}\)

\(\Rightarrow\widehat{IKH}=\widehat{ICH}\)

Mà \(\widehat{ICH}+\widehat{CHI}=90^0\)

\(\Rightarrow\widehat{IKH}+\widehat{CHI}=90^0\) (**)

Từ (*) và (**) \(\Rightarrow\widehat{IKH}=\widehat{DKH}\)

\(\Rightarrow KH\) là tia phân giác của \(\widehat{IKD}\)

Hay \(KC\) là tia phân giác của \(\widehat{IKD}\)

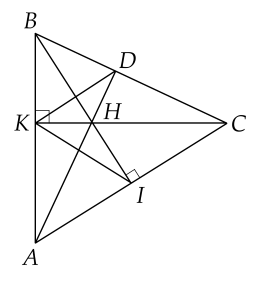
a) Vì tam giác 𝐾𝐵𝐶KBC vuông tại 𝐾K suy ra 𝐾𝐵𝐻^=90∘KBH=90∘

Vì 𝐶𝐼⊥𝐵𝐼CI⊥BI (gt) suy ra 𝐶𝑙𝐻^=90∘ClH=90∘

Xét △𝐾𝐵𝐻△KBH và △𝐶𝐻𝐼△CHI có:

𝐾𝐵𝐻^=𝐶𝐼𝐻^=90∘KBH=CIH=90∘;

𝐵𝐻𝐾^=𝐶𝐻𝐼^BHK=CHI (đối đỉnh)

Suy ra Δ𝐵𝐻𝐾∽Δ𝐶𝐻𝐼ΔBHK∽ΔCHI (g.g)

b) Ta có Δ𝐵𝐻𝐾∽Δ𝐶𝐻𝐼ΔBHK∽ΔCHI suy ra 𝐻𝐵𝐾^=𝐻𝐶𝐼^HBK=HCI (hai góc tương ứng) 

Mà 𝐵𝐻BH là tia phân giác của 𝐴𝐵𝐶^ABC nên 𝐻𝐵𝐾^=𝐻𝐵𝐶^HBK=HBC.

Do đó 𝐻𝐵𝐶^=𝐻𝐶𝐼^HBC=HCI.

Xét △𝐶𝐼𝐵△CIB và △𝐻𝐼𝐶△HIC có:

𝐶𝐼𝐵^CIB chung;

𝐼𝐵𝐶^=𝐻𝐶𝐼^IBC=HCI (cmt)

Vậy Δ𝐶𝐼𝐵≈Δ𝐻𝐼𝐶ΔCIB≈ΔHIC (g.g) suy ra 𝐶𝐼𝐻𝐼=𝐼𝐵𝐼𝐶HICI​=ICIB​

Hay 𝐶𝐼2=𝐻𝐼.𝐼𝐵CI2=HI.IB

c) Xét △𝐴𝐵𝐶△ABC có 𝐵𝐼⊥𝐴𝐶BI⊥AC; 𝐶𝐾⊥𝐴𝐵CK⊥AB; 𝐵𝐼∩𝐶𝐾={𝐻}BI∩CK={H}

Nên 𝐻H là trực tâm △𝐴𝐵𝐶△ABC suy ra 𝐴𝐻⊥𝐵𝐶AH⊥BC tại 𝐷D.

Từ đó ta có △𝐵𝐾𝐶∽△𝐻𝐷𝐶△BKC∽△HDC (g.g) nên 𝐶𝐵𝐶𝐻=𝐶𝐾𝐶𝐷CHCB​=CDCK​

Suy ra 𝐶𝐵𝐶𝐾=𝐶𝐻𝐶𝐷CKCB​=CDCH​ nên △𝐵𝐻𝐶∽△𝐾𝐷𝐶△BHC∽△KDC (c.g.c)

Khi đó 𝐻𝐵𝐶^=𝐷𝐾𝐶^HBC=DKC (hai góc tương ứng)

Chứng minh tương tự 𝐻𝐴𝐶^=𝐼𝐾𝐶^HAC=IKC

Mà 𝐻𝐴𝐶^=𝐻𝐵𝐶^HAC=HBC (cùng phụ 𝐴𝐶𝐵^ACB )

Suy ra  𝐷𝐾𝐶^=𝐼𝐾𝐶^ DKC=IKC.

Vậy 𝐾𝐶KC là tia phân giác của 𝐼𝐾𝐷^IKD.

a) Xét △ABC vuông tại A nên: AB² + AC² = BC² (Định lí Pythagore)
suy ra BC = \(\sqrt{AB^2+AC^2}\)

                 = \(\sqrt{6^2+8^2}\)

                 = 10
Vậy BC = 10

a: Sửa đề: AB=6

ΔABC vuông tại A

=>\(AB^2+AC^2=BC^2\)

=>\(\)\(BC^2=6^2+8^2=100=10^2\)

=>BC=10

b: Sửa đề: tính BD,CD

Xét ΔABC có AD là phân giác

nên \(\dfrac{DB}{AB}=\dfrac{DC}{AC}\)

=>\(\dfrac{DB}{6}=\dfrac{DC}{8}\)

=>\(\dfrac{DB}{3}=\dfrac{DC}{4}\)

mà DB+DC=BC=10

nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:

\(\dfrac{DB}{3}=\dfrac{DC}{4}=\dfrac{DB+DC}{3+4}=\dfrac{10}{7}\)

=>\(DB=3\cdot\dfrac{10}{7}=\dfrac{30}{7};DC=4\cdot\dfrac{10}{7}=\dfrac{40}{7}\)

a: Xét ΔHBA vuông tại H và ΔABC vuông tại A có

\(\widehat{HBA}\) chung

Do đó: ΔHBA~ΔABC

=>\(\dfrac{HB}{AB}=\dfrac{BA}{BC}\)

=>\(BA^2=BH\cdot BC\)

b: 

Xét ΔABC có

M,N lần lượt là trung điểm của AB,AC

=>MN là đường trung bình của ΔABC

=>MN//BC và MN=1/2BC

Xét tứ giác BMNC có MN//BC

nên BMNC là hình thang

Hình thang BMNC có \(\widehat{MBC}=\widehat{NCB}\)

nên BMNC là hình thang cân

ΔABC vuông cân tại A

mà AH là đường cao

nên AH là đường trung tuyến

=>\(AH=\dfrac{BC}{2}=MN\)

c: Xét ΔCAB có

CM,AH là các đường trung tuyến

CM cắt AH tại K

Do đó: K là trọng tâm của ΔCAB

=>\(AK=\dfrac{2}{3}AH=\dfrac{2}{3}\cdot\dfrac{1}{2}\cdot BC=\dfrac{1}{3}BC\)

=>BC=3AK

a: Xét ΔBAC vuông tại A và ΔBHA vuông tại H có

\(\widehat{ABC}\) chung

Do đó: ΔBAC~ΔBHA

=>\(\dfrac{BA}{BH}=\dfrac{BC}{BA}\)

=>\(BA^2=BH\cdot BC\)

b: 

Xét ΔBAC vuông tại A và ΔACD vuông tại C có

\(\widehat{ABC}=\widehat{CAD}\left(=90^0-\widehat{HAB}\right)\)

Do đó: ΔBAC~ΔACD

=>\(\dfrac{AC}{CD}=\dfrac{BA}{AC}\)

=>\(AC^2=AB\cdot CD\)

a: Xét ΔABC vuông tại A và ΔHBA vuông tại H có

\(\widehat{ABC}\) chung

Do đó: ΔABC~ΔHBA

=>\(\dfrac{AC}{HA}=\dfrac{BC}{BA}=\dfrac{AB}{HB}\)

=>\(AB\cdot HA=AC\cdot HB\)

b: ΔABC vuông tại A

=>\(AB^2+AC^2=BC^2\)

=>\(BC=\sqrt{15^2+20^2}=25\left(cm\right)\)

\(\dfrac{BC}{BA}=\dfrac{AC}{HA}\)

=>\(HA=\dfrac{AB\cdot AC}{BC}=\dfrac{15\cdot20}{25}=\dfrac{300}{25}=12\left(cm\right)\)
=>\(HB=\sqrt{15^2-12^2}=9\left(cm\right)\)

c: 

Xét ΔBAH có BI là phân giác

nên \(\dfrac{IA}{IH}=\dfrac{BA}{BH}\left(1\right)\)

Xét ΔBAC có BD là phân giác

nên \(\dfrac{DC}{DA}=\dfrac{BC}{BA}\left(2\right)\)

Ta có: ΔBHA~ΔBAC

=>\(\dfrac{BA}{BC}=\dfrac{BH}{BA}\)

=>\(\dfrac{BC}{BA}=\dfrac{BA}{BH}\left(3\right)\)

Từ (1),(2),(3) suy ra \(\dfrac{IA}{IH}=\dfrac{DC}{DA}\)

=>\(IA\cdot DA=DC\cdot IH\)

Bài 2:

1: ĐKXĐ: \(x\notin\left\{1;-1\right\}\)

\(A=\left(\dfrac{x+3}{2x+2}+\dfrac{3}{1-x^2}-\dfrac{x+1}{2x-2}\right):\dfrac{3}{2x^2-2}\)

\(=\left(\dfrac{x+3}{2\left(x+1\right)}-\dfrac{3}{\left(x-1\right)\left(x+1\right)}-\dfrac{x+1}{2\left(x-1\right)}\right)\cdot\dfrac{2\left(x-1\right)\left(x+1\right)}{3}\)

\(=\dfrac{\left(x+3\right)\left(x-1\right)-6-\left(x+1\right)^2}{2\left(x+1\right)\left(x-1\right)}\cdot\dfrac{2\left(x-1\right)\left(x+1\right)}{3}\)

\(=\dfrac{x^2+2x-3-6-x^2-2x-1}{3}=\dfrac{-10}{3}\) không phụ thuộc vào biến x

Bài 4:

1: 

Xét ΔCAF vuông tại A và ΔCHE vuông tại H có

\(\widehat{ACF}=\widehat{HCE}\)

Do đó: ΔCAF~ΔCHE

2: Ta có ΔCAF~ΔCHE

=>\(\widehat{CFA}=\widehat{CEH}\)

mà \(\widehat{CEH}=\widehat{AEF}\)(hai góc đối đỉnh)

nên \(\widehat{AEF}=\widehat{AFE}\)

=>ΔAEF cân tại A

Xét ΔCAH vuông tại H và ΔCBA vuông tại A có

\(\widehat{ACH}\) chung

Do đó: ΔCAH~ΔCBA

=>\(\dfrac{CA}{CB}=\dfrac{CH}{CA}\left(1\right)\)

Xét ΔCAH có CE là phân giác

nên \(\dfrac{HE}{AE}=\dfrac{CH}{CA}\left(2\right)\)

Xét ΔCAB có CF là phân giác

nên \(\dfrac{AF}{FB}=\dfrac{CA}{CB}\left(3\right)\)

Từ (1),(2),(3) suy ra \(\dfrac{HE}{AE}=\dfrac{AF}{FB}\)

=>\(HE\cdot FB=AE\cdot AF=AE^2\)

Gọi A là biến cố "Lấy được viên bi màu đỏ"

Trong túi có 8 viên màu đỏ nên n(A)=8

=>\(P\left(A\right)=\dfrac{8}{19}\)

Nghiện của phương trình 2x + 06= 0 là 

1: 

a: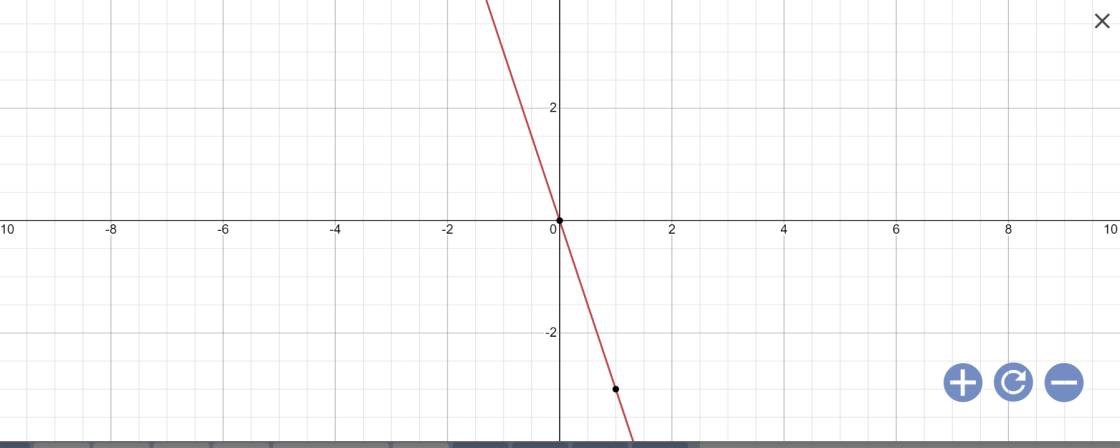 

b: Vì (d3)//(d2) nên \(\left\{{}\begin{matrix}a=1\\b\ne2\end{matrix}\right.\)

Vậy: (d3): y=x+b

Thay x=-1 và y=3 vào (d3), ta được:

b-1=3

=>b=4

Vậy: (d3): y=x+4

Bài 2:

Gọi số sản phẩm tổ 1 phải sản xuất theo kế hoạch là x(sản phẩm)

(ĐIều kiện: \(x\in Z^+\))

Số sản phẩm tổ 2 phải sản xuất theo kế hoạch là:

900-x(sản phẩm)

Số sản phẩm thực tế tổ 1 làm được là:

\(x\left(1+20\%\right)=1,2x\left(sảnphẩm\right)\)

Số sản phẩm thực tế tổ 2 làm được là:

\(\left(900-x\right)\left(1+15\%\right)=1,15\left(900-x\right)\left(sảnphẩm\right)\)

Tổng số sản phẩm là 1055 sản phẩm nên ta có:

1,2x+1,15(900-x)=1055

=>0,05x+1035=1055

=>0,05x=20

=>x=400(nhận)

Vậy: số sản phẩm tổ 1 phải sản xuất theo kế hoạch là 400 sản phẩm

số sản phẩm tổ 2 phải sản xuất theo kế hoạch là 900-400=500 sản phẩm

1b) Vì đường thẳng (�3):�=��+�(d3
​):y=ax+b đi qua điểm �(−1;3)A(−1;3) và song song với (�2)(d2
​).

suy ra : x=-1 ; y=3 và a=1;b khác 2

thay x=-1 ; y=3 và a=1 vào đường thẳng (�3):�=��+�(d3
​):y=ax+b ta được :

1(-1)+b=3

b=4(TM)

2)bí bì

a) \(2x=7+x\)

\(\Leftrightarrow2x-x=7\)

\(\Leftrightarrow x=7\)

Vậy \(S=\{7\}\)

b) \(\dfrac{x-3}{5}+\dfrac{1+2x}{3}=6\)

\(\Leftrightarrow\dfrac{3\left(x-3\right)}{15}+\dfrac{5\left(1+2x\right)}{15}=6\)

\(\Leftrightarrow\dfrac{3x-9+5+10x}{15}=6\)

\(\Leftrightarrow13x-4=90\)

\(\Leftrightarrow13x=94\)

\(\Leftrightarrow x=\dfrac{94}{13}\)

Vậy \(S=\left\{\dfrac{94}{13}\right\}\).