Pt: \(x^2+5x+2=0\)

Theo vi-ét: \(\left\{{}\begin{matrix}x_1+x_2=\dfrac{-5}{1}=-5\\x_1x_2=\dfrac{2}{1}=2\end{matrix}\right.\)

a) \(x^2_1+x_2^2=\left(x_1+x_2\right)^2-2x_1x_2=\left(-5\right)^2-2\cdot2=25-4=21\)

b) \(x_1^3+x_2^3=\left(x_1+x_2\right)\left(x_1^2+x_1x_2+x_2^2\right)=\left(x_1+x_2\right)\left[\left(x_1+x_2\right)^2-2x_1x_2-x_1x_2\right]\)

\(=\left(x_1+x_2\right)\left[\left(x_1+x_2\right)^2-3x_1x_2\right]=\left(-5\right)\cdot\left[\left(-5\right)^2-3\cdot2\right]=-95\)  

c) \(\left|x_1-x_2\right|=\sqrt{\left|x_1-x_2\right|^2}=\sqrt{x_1^2+x_2^2-2\left|x_1x_2\right|}\)

\(=\sqrt{\left(x_1+x_2\right)^2-2x_1x_2-2\left|x_1x_2\right|}=\sqrt{\left(-5\right)^2-2\cdot2-2\cdot\left|2\right|}=\sqrt{17}\) 

d) \(x_1^2x_2^3+x_2^2x_1^3=x_1^2x_2^2\left(x_1+x_2\right)=\left(x_1x_2\right)^2\cdot\left(x_1+x_2\right)=2^2\cdot\left(-5\right)=-20\)

Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=-5\\x_1x_2=2\end{matrix}\right.\)

\(x_1^2+x_2^2=\left(x_1+x_2\right)^2-2x_1x_2=\left(-5\right)^2-2.2=21\)

\(x_1^3+x_2^3=\left(x_1+x_2\right)^3-3x_1x_2\left(x_1+x_2\right)=\left(-5\right)^3-3.2.\left(-5\right)=-95\)

\(\left|x_1-x_2\right|=\sqrt{\left(x_1-x_2\right)^2}=\sqrt{\left(x_1+x_2\right)^2-4x_1x_2}=\sqrt{\left(-5\right)^2-4.2}=\sqrt{17}\)

\(x_1^2x_2^3+x_1^3x_2^2=\left(x_1x_2\right)^2\left(x_1+x_2\right)=2^2.\left(-5\right)=-20\)

a:

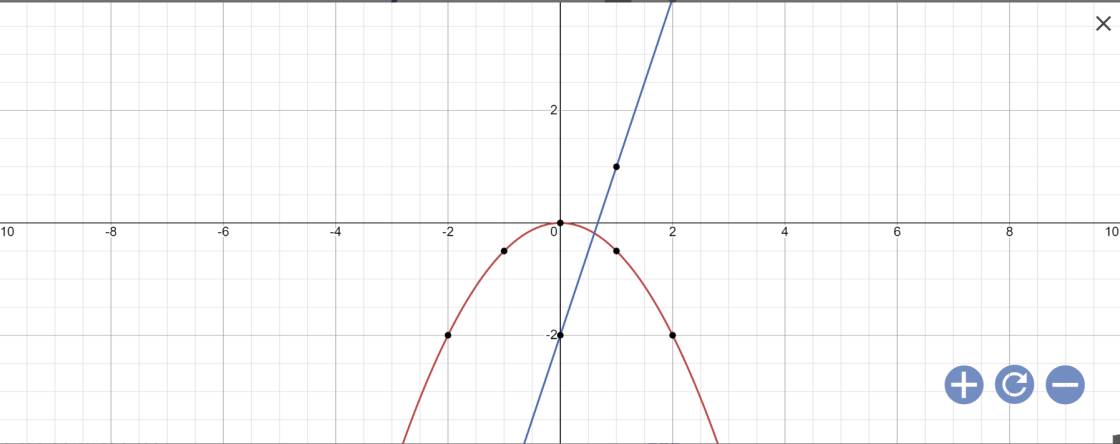
Phương trình hoành độ giao điểm là:

\(-\dfrac{1}{2}x^2=3x-2\)

=>\(-x^2=6x-4\)

=>\(x^2+6x-4=0\)

=>\(\left(x+3\right)^2-13=0\)

=>\(\left(x+3\right)^2=13\)

=>\(\left[{}\begin{matrix}x+3=\sqrt{13}\\x+3=-\sqrt{13}\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\sqrt{13}-3\\x=-\sqrt{13}-3\end{matrix}\right.\)

Thay \(x=\sqrt{13}-3\) vào y=3x-2, ta được:

\(y=3\left(\sqrt{13}-3\right)-2=3\sqrt{13}-11\)

Thay \(x=-\sqrt{13}-3\) vào y=3x-2, ta được:

\(y=3\left(-\sqrt{13}-3\right)-2=-3\sqrt{13}-11\)

Vậy: (P) cắt (d) tại \(C\left(\sqrt{13}-3;3\sqrt{13}-11\right);D\left(-\sqrt{13}-3;-3\sqrt{13}-11\right)\)

b: Thay x=-4 vào (P), ta được: 

\(y=-\dfrac{1}{2}\cdot\left(-4\right)^2=-\dfrac{1}{2}\cdot16=-8\)

Vậy: A(3;1); B(-4;-8)

Thay x=3 và y=1 vào (d'), ta được:

\(3\cdot a+b=1\)(1)

Thay x=-4 và y=-8 vào (d'), ta được:

\(a\cdot\left(-4\right)+b=-8\left(2\right)\)

Từ (1) và (2) ta có hệ phương trình:

\(\left\{{}\begin{matrix}3a+b=1\\-4a+b=-8\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}7a=9\\3a+b=1\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}a=\dfrac{9}{7}\\b=1-3a=1-\dfrac{27}{7}=-\dfrac{20}{7}\end{matrix}\right.\)

là bằng 6 đó

6

a: Xét tứ giác ABOC có \(\widehat{ABO}+\widehat{ACO}=90^0+90^0=180^0\)

nên ABOC là tứ giác nội tiếp

b: Xét (O) có

\(\widehat{ABM}\) là góc tạo bởi tiếp tuyến BA và dây cung BM

\(\widehat{BNM}\) là góc nội tiếp chắn cung BM

Do đó: \(\widehat{ABM}=\widehat{BNM}\)

Xét ΔABM và ΔANB có

\(\widehat{ABM}=\widehat{ANB}\)

\(\widehat{BAM}\) chung

Do đó: ΔABM~ΔANB

=>\(\dfrac{AB}{AN}=\dfrac{AM}{AB}\)

=>\(AB^2=AM\cdot AN\)

a: Xét tứ giác ABOC có \(\widehat{OBA}+\widehat{OCA}=90^0+90^0=180^0\)

nên ABOC là tứ giác nội tiếp

b: Xét (O) có

\(\widehat{NBA}\) là góc tạo bởi tiếp tuyến BA và dây cung BN

\(\widehat{BMN}\) là góc nội tiếp chắn cung BN

Do đó: \(\widehat{NBA}=\widehat{BMN}\)

mà \(\widehat{BMN}=\widehat{KAN}\)(hai góc so le trong, BM//AC)

nên \(\widehat{KAN}=\widehat{KBA}\)

Xét ΔKAN và ΔKBA có

\(\widehat{KAN}=\widehat{KBA}\)

\(\widehat{AKN}\) chung

Do đó: ΔKAN~ΔKBA

=>\(\dfrac{KA}{KB}=\dfrac{KN}{KA}\)

=>\(KA^2=KB\cdot KN\)(1)

c: Xét (O) có

\(\widehat{KCN}\) là góc tạo bởi tiếp tuyến CK và dây cung CN

\(\widehat{CBN}\) là góc nội tiếp chắn cung CN

Do đó: \(\widehat{KCN}=\widehat{CBN}=\widehat{KBC}\)

Xét ΔKCN và ΔKBC có

\(\widehat{KCN}=\widehat{KBC}\)

\(\widehat{CKN}\) chung

Do đó: ΔKCN~ΔKBC

=>\(\dfrac{KC}{KB}=\dfrac{KN}{KC}\)

=>\(KC^2=KB\cdot KN\left(2\right)\)

Từ (1) và (2) suy ra KA=KC

=>K là trung điểm của AC

ΔOCA vuông tại C

=>\(CO^2+CA^2=OA^2\)

=>\(CA^2=\left(3R\right)^2-R^2=8R^2\)

=>\(CA=R\cdot2\sqrt{2}\)

=>\(KA=R\sqrt{2}\)

d: Gọi giao điểm của MN và OE là I, giao điểm của BC và OA là H

Xét (O) có

EM,EN là các tiếp tuyến

Do đó: EM=EN

=>E nằm trên đường trung trực của MN(3)

Ta có: OM=ON

=>O nằm trên đường trung trực của MN(4)

Từ (3) và (4) suy ra OE là đường trung trực của MN

=>OE\(\perp\)MN tại I và I là trung điểm của MN

Xét (O) có

AB,AC là các tiếp tuyến

Do đó: AB=AC

=>A nằm trên đường trung trực của BC(5)

ta có: OB=OC

=>O nằm trên đường trung trực của BC(6)

Từ (5),(6) suy ra OA là đường trung trực của BC

=>OA\(\perp\)BC tại H

Xét ΔOBA vuông tại B có BH là đường cao

nên \(OH\cdot OA=OB^2=R^2\left(7\right)\)

Xét ΔONE vuông tại N có NI là đường cao

nên \(OI\cdot OE=ON^2\left(8\right)\)

Từ (7) và (8) suy ra \(OH\cdot OA=OI\cdot OE\)

=>\(\dfrac{OH}{OI}=\dfrac{OE}{OA}\)

Xét ΔOHE và ΔOIA có

\(\dfrac{OH}{OI}=\dfrac{OE}{OA}\)

\(\widehat{HOE}\) chung

Do đó: ΔOHE~ΔOIA

=>\(\widehat{OHE}=\widehat{OIA}=90^0\)

=>\(\widehat{OHE}=\widehat{OHB}=90^0\)

=>H,B,E thẳng hàng

mà B,H,C thẳng hàng

nên E,B,C thẳng hàng

Lời giải:
A. Khẳng định này sai do khi $y=0$ thì $2x=4+y=4\Rightarrow x=2$. PT có nghiệm $(x,y)=(2,0)$

B. Sai. PT có nghiệm, chả hạn $(x,y)=(2,0)$

C. Đúng. $x=\frac{y+4}{2}$. Với $y$ là số thực bất kỳ thì ta luôn có $x$ tương ứng.

D. Sai. $2x-y=4\Rightarrow 2x=y+4$

Bạn nên gõ đề bằng công thức toán (biểu tượng $\sum$ góc trái khung soạn thảo) để mọi người hiểu đề và hỗ trợ nhanh hơn nhé.

a: Thay m=-1 vào phương trình, ta được:

\(x^2-2\left(-1-1\right)x+\left(-1\right)+1=0\)

=>\(x^2+4x=0\)

=>x(x+4)=0

=>\(\left[{}\begin{matrix}x=0\\x=-4\end{matrix}\right.\)

b: \(\text{Δ}=\left[-2\left(m-1\right)\right]^2-4\left(m+1\right)\)

\(=4\left(m^2-2m+1\right)-4\left(m+1\right)\)

\(=4\left(m^2-3m\right)\)

Để phương trình có hai nghiệm thì Δ>=0

=>m^2-3m>=0

=>m(m-3)>=0

=>\(\left[{}\begin{matrix}m>=3\\m< =0\end{matrix}\right.\)

Theo Vi-et, ta có:

\(x_1+x_2=-\dfrac{b}{a}=2\left(m-1\right);x_1x_2=m+1\)

\(\dfrac{x_1}{x_2}+\dfrac{x_2}{x_1}=4\)

=>\(\dfrac{x_1^2+x_2^2}{x_1x_2}=4\)

=>\(\left(x_1+x_2\right)^2-2x_1x_2=4x_1x_2\)

=>\(\left(2m-2\right)^2-6\left(m+1\right)=0\)

=>\(4m^2-8m+4-6m-6=0\)

=>\(4m^2-14m-2=0\)

=>\(\left[{}\begin{matrix}m=\dfrac{7+\sqrt{57}}{4}\left(nhận\right)\\m=\dfrac{7-\sqrt{57}}{4}\left(nhận\right)\end{matrix}\right.\)