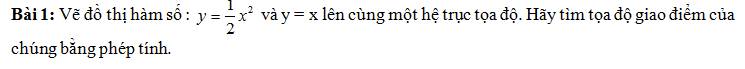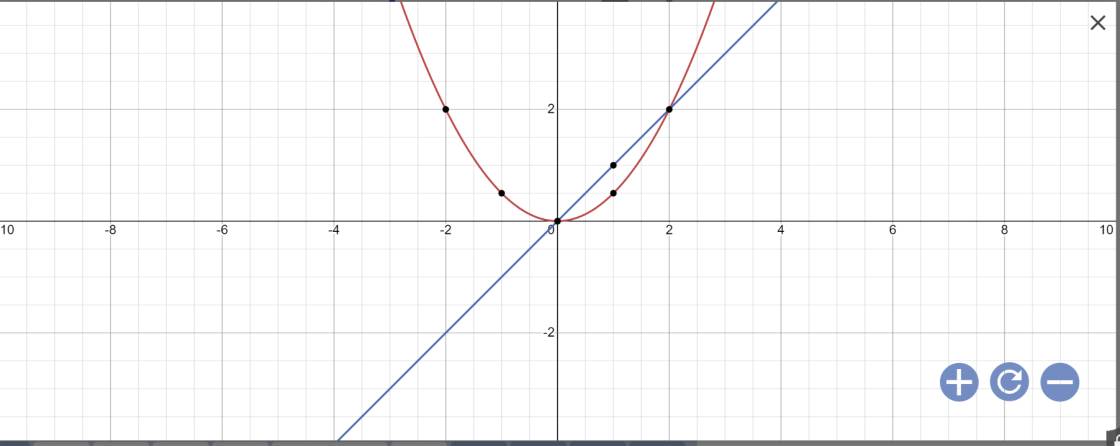
Phương trình hoành độ giao điểm là:

\(\dfrac{1}{2}x^2=x\)

=>\(\dfrac{1}{2}x^2-x=0\)

=>\(x\left(\dfrac{1}{2}x-1\right)=0\)

=>\(\left[{}\begin{matrix}x=0\\x=2\end{matrix}\right.\)

Thay x=0 vào y=x, ta được:

y=x=0

Thay x=2 vào y=x, ta được:

y=x=2

Vậy: Tọa độ giao điểm là O(0;0); A(2;0)

Bài 6:

Gọi số học sinh của lớp 9A và lớp 9B lần lượt là a(bạn),b(bạn)

(Điều kiện: \(a,b\in Z^+\))

Tổng số học sinh là 105 nên a+b=105(1)

Số cây lớp 9A trồng được là 4a(cây)

Số cây lớp 9B trồng được là 5b(cây)

Tổng số cây hai lớp trồng được là 472 cây nên 4a+5b=472(2)

Từ (1) và (2) ta có hệ phương trình:

\(\left\{{}\begin{matrix}a+b=105\\4a+5b=472\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}4a+4b=420\\4a+5b=472\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}-b=-52\\a+b=105\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}b=52\\a=105-52=53\end{matrix}\right.\left(nhận\right)\)

Vậy: số học sinh của lớp 9A và lớp 9B lần lượt là 53 bạn và 52 bạn

Bài 5:

Gọi số học sinh của lớp 9B và lớp 9C lần lượt là a(bạn),b(bạn)

(Điều kiện: \(a,b\in Z^+\))

Tổng số học sinh là 78 nên a+b=78(3)

Số cây lớp 9B trồng được là 3a(cây)

Số cây lớp 9C trồng được là 4b(cây)

Tổng số cây hai lớp trồng được là 274 cây nên 3a+4b=274(4)

Từ (3) và (4) ta có hệ phương trình:

\(\left\{{}\begin{matrix}3a+4b=274\\a+b=78\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}3a+4b=274\\3a+3b=234\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}b=40\\a=78-b=78-40=38\end{matrix}\right.\left(nhận\right)\)

Vậy: số học sinh của lớp 9B và lớp 9C lần lượt là 38 bạn và 40 bạn

Lời giải:

Áp dụng BĐT AM-GM:

$abc\leq \left(\frac{a+b+c}{3}\right)^3=(\frac{1}{3})^3=\frac{1}{27}$

$(a+b)(b+c)(c+a)\leq \left(\frac{a+b+b+c+c+a}{3}\right)^3=\left(\frac{2(a+b+c)}{3}\right)^3=(\frac{2}{3})^3=\frac{8}{27}$
$\Rightarrow abc(a+b)(b+c)(c+a)\leq \frac{1}{27}.\frac{8}{27}=\frac{8}{729}$

Dấu "=" xảy ra khi $a=b=c=\frac{1}{3}$

Như vậy đề có vẻ sai sai đó bạn.

Đề tham khảo chắc chưa được thẩm định kĩ.

\(\left\{{}\begin{matrix}45\left(t+\dfrac{1}{2}\right)=S\\60\left(t-\dfrac{3}{4}\right)=S\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}45\left(t+\dfrac{1}{2}\right)=60\left(t-\dfrac{3}{4}\right)\\S=45\left(t+\dfrac{1}{2}\right)\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}3\left(t+\dfrac{1}{2}\right)=4\left(t-\dfrac{3}{4}\right)\\S=45\left(t+\dfrac{1}{2}\right)\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}3t+1,5=4t-3\\S=45\left(t+0,5\right)\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}-t=-4,5\\S=45\left(t+0,5\right)\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}t=4,5\\S=45\left(4,5+0,5\right)=45\cdot5=225\end{matrix}\right.\)

a: Xét tứ giác ABOC có \(\widehat{OBA}+\widehat{OCA}=90^0+90^0=180^0\)

nên ABOC là tứ giác nội tiếp

Xét (O) có

AB,AC là các tiếp tuyến

Do đó: AB=AC

=>A nằm trên đường trung trực của BC(1)

Ta có: OB=OC

=>O nằm trên đường trung trực của BC(2)

Từ (1) và (2) suy ra OA là đường trung trực của BC

=>OA\(\perp\)BC tại H và H là trung điểm của BC

b: Xét (O) có

ΔCFE nội tiếp

CE là đường kính

Do đó: ΔCFE vuông tại F

=>CF\(\perp\)FE tại F

=>CF\(\perp\)AE tại F

Xét ΔCAE vuông tại C có CF là đường cao

nên \(AF\cdot AE=AC^2\)

=>\(AF\cdot AE=AB^2\left(3\right)\)

Xét ΔABO vuông tại B có BH là đường cao

nên \(AH\cdot AO=AB^2\left(4\right)\)

Từ (3) và (4) suy ra \(AF\cdot AE=AH\cdot AO\)

=>\(\dfrac{AF}{AO}=\dfrac{AH}{AE}\)

Xét ΔAFH và ΔAOE có

\(\dfrac{AF}{AO}=\dfrac{AH}{AE}\)

\(\widehat{FAH}\)chung

Do đó: ΔAFH~ΔAOE

=>\(\widehat{AFH}=\widehat{AOE}\)

mà \(\widehat{AFH}+\widehat{EFH}=180^0\)(hai góc kề bù)

nên \(\widehat{EOH}+\widehat{EFH}=180^0\)

=>EOHF là tứ giác nội tiếp

ai giúp e với ạ :*(

a: Xét (O) có

ΔPEQ nội tiếp

PQ là đường kính 

Do đó: ΔPEQ vuông tại E

Xét tứ giác HEQS có \(\widehat{HEQ}+\widehat{HSQ}=90^0+90^0=180^0\)

nên HEQS là tứ giác nội tiếp

b: Xét ΔSPH vuông tại S và ΔSFQ vuông tại S có

\(\widehat{SPH}=\widehat{SFQ}\left(=90^0-\widehat{Q}\right)\)

Do đó: ΔSPH~ΔSFQ

=>\(\dfrac{SP}{SF}=\dfrac{SH}{SQ}\)

=>\(SP\cdot SQ=SH\cdot SF\)

ai giúp mik nhanh vs ạ mik tick