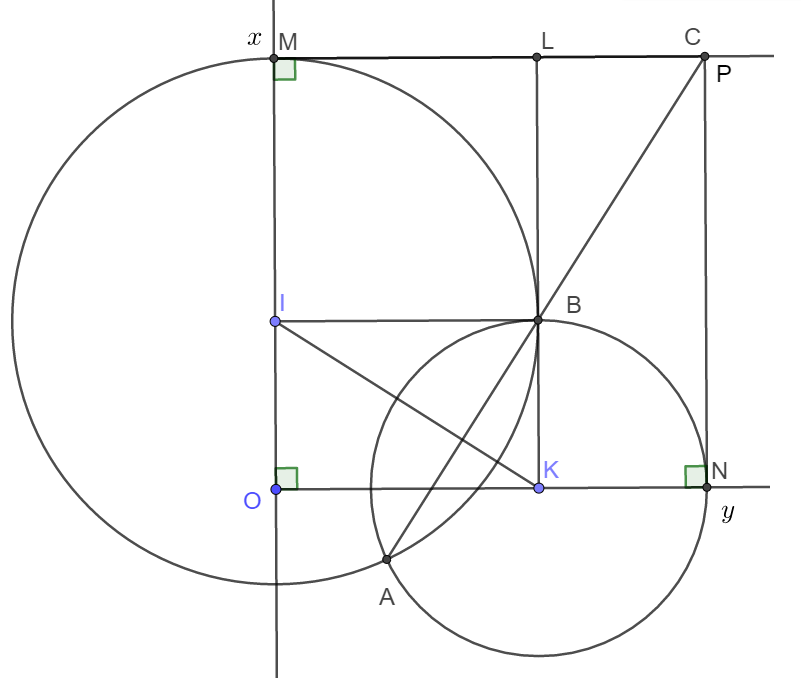
Cho tam giác ABC vuông tại C Vẽ Đường Tròn tâm O đường kính AC cắt AB tại D Gọi M là điểm chính của cung nhỏ CD nối AM cắt BC tại N nối ĐM cắt BC tại E tia phân giác của góc MAD cắt BC tại I cắt MD tại K
a) chứng minh tứ giác BDMN
b) chứng minh tâm giác EIK cân
c) chứng minh MN . AB = MC . NB