Cho tam giác ABC có góc A=80° , góc B=60° . Hai tia phân giác của góc B và C cắt nhau tại I. Vẽ tia phân giác ngoài tại đỉnh B cắt tia CI tại D. Số đo góc BDC là ?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Bài giải
Số quả táo của anh là :
( 10 + 2 ) : 2 = 6 ( quả )
Số quả táo của em là :
10 - 6 = 4 ( quả )
Đáp số : anh : 6 quả táo
em : 4 quả táo
Mik làm hơi chậm, xin lỗi bạn nhiều

1200 = 2⁴.3.5²
Số ước của 1200:
(4 + 1).(1 + 1).(2 + 1) = 30 (ước)

a: Xét (O) có
ΔBAC nội tiếp
BC là đường kính
Do đó: ΔBAC vuông tại A
=>PA\(\perp\)BD tại A
Xét (O) có
ΔCIB nội tiếp
CB là đường kính
Do đó: ΔCIB vuông tại I
Xét tứ giác ADHC có \(\widehat{DAC}+\widehat{DHC}=90^0+90^0=180^0\)
nên ADHC là tứ giác nội tiếp
b: Xét ΔDBP có
PA,BH là các đường cao
PA cắt BH tại C
Do đó: C là trực tâm của ΔDBP
=>DC\(\perp\)BP
mà CI\(\perp\)BP
mà DC,CI có điểm chung là C
nên D,C,I thẳng hàng
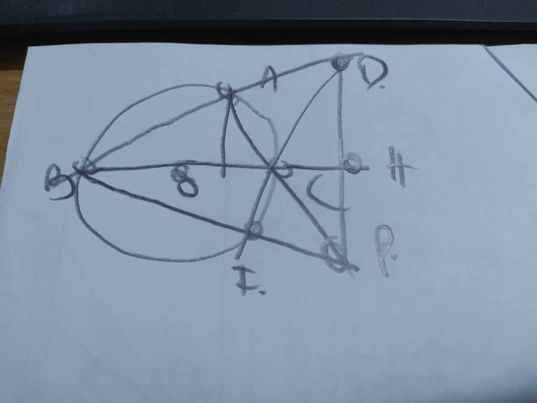
| GT | (O) có đường kính BC \(A\in\left(O\right);AP>AC;P\in AC\) PB\(\cap\)(O)={I} PH\(\perp\)BC tại H, PH cắt BA tại D |
| KL | a: ACHD nội tiếp b: D,C,I thẳng hàng |

a) Thời gian người đó đi hết quãng đường AB:
10 giờ 9 phút - 7 giờ 45 phút = 2 giờ 24 phút = 2,4 (giờ)
Quãng đường AB dài:
35 × 2,4 = 84 (km)
b) Vận tốc lúc về:
35 × 6/5 = 42 (km/giờ)
Thời gian người đó đi từ B về A:
84 : 42 = 2 (giờ)

\(\dfrac{787878}{666666}=\dfrac{787878:60606}{666666:60606}=\dfrac{13}{11}\)

a: Xét tứ giác BEDC có \(\widehat{BEC}=\widehat{BDC}=90^0\)
nên BEDC là tứ giác nội tiếp
b: Xét (O) có
\(\widehat{CNM}\) là góc nội tiếp chắn cung CM
\(\widehat{CBM}\) là góc nội tiếp chắn cung CM
Do đó: \(\widehat{CNM}=\widehat{CBM}\)
mà \(\widehat{CBM}=\widehat{CED}\)(BEDC nội tiếp)
nên \(\widehat{HED}=\widehat{HNM}\)
=>ED//MN
c: Kẻ Ax là tiếp tuyến của (O) tại A
Xét (O) có
\(\widehat{xAC}\) là góc tạo bởi tiếp tuyến Ax và dây cung AC
\(\widehat{ABC}\) là góc nội tiếp chắn cung AC
Do đó: \(\widehat{xAC}=\widehat{ABC}\)
mà \(\widehat{ABC}=\widehat{ADE}\left(=180^0-\widehat{EDC}\right)\)
nên \(\widehat{xAC}=\widehat{ADE}\)
=>Ax//DE
=>OA\(\perp\)DE

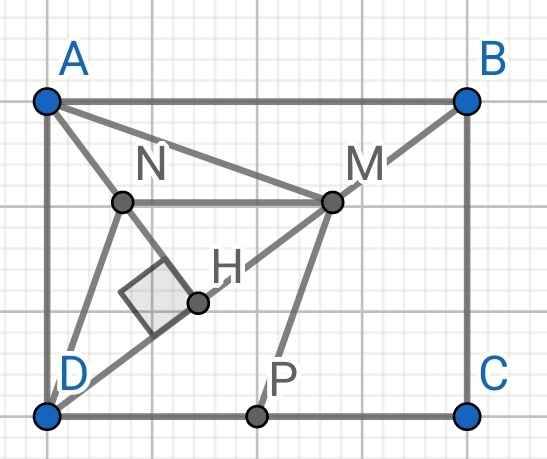
a) Do ABCD là hình chữ nhật (gt)
⇒ AB // CD
⇒ ∠ABH = ∠BDC (so le trong)
Xét hai tam giác vuông: ∆AHB và ∆BCD có:
∠ABH = ∠BDC (cmt)
⇒ ∆AHB ∽ ∆BCD (g-g)
b) ∆ABD vuông tại A
⇒ BD² = AB² + AD² (Pythagore)
= AB² + BC²
= 8² + 6²
= 100
⇒ BD = 10 (cm)
Do ∆AHB ∽ ∆BCD (cmt)
⇒ AH/BC = AB/BD
⇒ AH/6 = 8/10
⇒ AH = 8.6 : 10 = 4,8 (cm)
∆AHD vuông tại H
⇒ AD² = AH² + DH² (Pythagore)
⇒ DH² = AD² - AH²
= 6² - 4,8²
= 12,96
⇒ DH = 3,6 (cm)
c) Gọi N là trung điểm của AH
∆AHB có:
M là trung điểm của BH (gt)
N là trung điểm của AH
⇒ MN là đường trung bình của ∆ABH
⇒ MN // AB
Mà AB // CD (cmt)
⇒ MN // CD
⇒ MN // PD (1)
Do MN là đường trung bình của ∆ABH (cmt)
⇒ MN = AB : 2
Mà AB = CD (do ABCD là hình chữ nhật)
⇒ MN = CD : 2
⇒ MN = PD (do P là trung điểm của CD) (2)
Từ (1) và (2) ⇒ MNDP là hình bình hành
⇒ DN // MP
Do MN // AB (cmt)
AB ⊥ AD (do ABCD là hình chữ nhật)
⇒ MN ⊥ AD
∆ADM có:
MN ⊥ AD (cmt)
⇒ MN là đường cao của ∆ADM
Lại có AH ⊥ BD (gt)
⇒ AH ⊥ DM
⇒ AH là đường cao thứ hai của ∆ADM
Mà AH và MN cắt nhau tại N
⇒ DN là đường cao thứ ba của ∆ADM
⇒ DN ⊥ AM
Mà DN // MP (cmt)
⇒ AM ⊥ MP

a: C thuộc đoạn AB
=>C nằm giữa A và B
=>AC+CB=AB
=>CB+1=5
=>CB=4(cm)
b: D là trung điểm của BC
=>\(BD=CD=\dfrac{BC}{2}=2\left(cm\right)\)
c: AC+CD=AD
=>AD=1+2=3(cm)
Vì AD và AE là hai tia đối nhau
nên A nằm giữa D và E
mà AD=AE(=3cm)
nên A là trung điểm của DE
d: Ta có: \(\widehat{BAy}=60^0\)
\(\widehat{BAx}=180^0\)
mà 60<180
nên \(\widehat{BAy}< \widehat{BAx}\)

