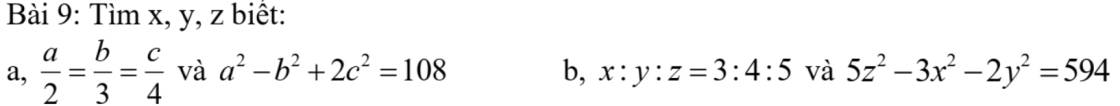 giải giúp mình với mình cần gấp
giải giúp mình với mình cần gấp
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: \(\dfrac{2x}{3}=\dfrac{3y}{4}=\dfrac{4z}{5}\)
=>\(\dfrac{x}{\dfrac{3}{2}}=\dfrac{y}{\dfrac{4}{3}}=\dfrac{z}{\dfrac{5}{4}}\)
mà x+y+z=49
nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{x}{\dfrac{3}{2}}=\dfrac{y}{\dfrac{4}{3}}=\dfrac{z}{\dfrac{5}{4}}=\dfrac{x+y+z}{\dfrac{3}{2}+\dfrac{4}{3}+\dfrac{5}{4}}=\dfrac{49}{\dfrac{49}{12}}=12\)
=>\(x=12\cdot\dfrac{3}{2}=18;y=12\cdot\dfrac{4}{3}=16;z=12\cdot\dfrac{5}{4}=15\)
b: \(\dfrac{6}{11}x=\dfrac{9}{2}y=\dfrac{18}{5}z\)
=>\(\dfrac{x}{\dfrac{11}{6}}=\dfrac{y}{\dfrac{2}{9}}=\dfrac{z}{\dfrac{5}{18}}\)
mà -x+y+z=-120
nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{x}{\dfrac{11}{6}}=\dfrac{y}{\dfrac{2}{9}}=\dfrac{z}{\dfrac{5}{18}}=\dfrac{-x+y+z}{-\dfrac{11}{6}+\dfrac{2}{9}+\dfrac{5}{18}}=\dfrac{-120}{-\dfrac{4}{3}}=90\)
=>\(x=90\cdot\dfrac{11}{6}=165;y=90\cdot\dfrac{2}{9}=20;z=90\cdot\dfrac{5}{18}=25\)
a) \(\dfrac{2x}{3}=\dfrac{3y}{4}=\dfrac{4z}{5}\Rightarrow\dfrac{x}{\dfrac{3}{2}}+\dfrac{y}{\dfrac{4}{3}}+\dfrac{z}{\dfrac{5}{4}}\)
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
\(\dfrac{x}{\dfrac{3}{2}}+\dfrac{y}{\dfrac{4}{3}}+\dfrac{z}{\dfrac{5}{4}}=\dfrac{x+y+z}{\dfrac{3}{2}+\dfrac{4}{3}+\dfrac{5}{4}}=\dfrac{49}{\dfrac{49}{12}}=12\)
\(\Rightarrow\dfrac{x}{\dfrac{3}{2}}=12\Rightarrow x=\dfrac{3}{2}\cdot12=18\)
\(\Rightarrow\dfrac{y}{\dfrac{4}{3}}=12\Rightarrow y=\dfrac{4}{3}\cdot12=16\)
\(\Rightarrow\dfrac{z}{\dfrac{5}{4}}=12\Rightarrow z=12\cdot\dfrac{5}{4}=15\)
Vậy: ...

\(\dfrac{3x}{8}=\dfrac{3y}{64}=\dfrac{3z}{216}\)
=>\(\dfrac{x}{8}=\dfrac{y}{64}=\dfrac{z}{216}\)
=>\(\dfrac{x}{2}=\dfrac{y}{16}=\dfrac{z}{54}\)
=>\(\dfrac{x}{1}=\dfrac{y}{8}=\dfrac{z}{27}\)
Đặt \(\dfrac{x}{1}=\dfrac{y}{8}=\dfrac{z}{27}=k\)
=>x=k; y=8k; z=27k
\(2x^2+2y^2-z^2=1\)
=>\(2k^2+2\cdot\left(8k\right)^2-\left(27k\right)^2=1\)
=>\(2k^2+128k^2-729k^2=1\)
=>\(k^2=-\dfrac{1}{599}\)(vô lý)
Vậy: KHông có bộ số (x;y;z) nào thỏa mãn yêu cầu đề bài

TH1: p=2
\(p^2+8=2^2+8=12\) không là số nguyên tố
=>Loại
TH2: p=3
\(p^2+8=3^2+8=17\) là số nguyên tố
\(p^2+2=3^2+2=11\) là số nguyên tố
=>Nhận
TH3: p=3k+1
\(p^2+8=\left(3k+1\right)^2+8=9k^2+6k+9=3\left(3k^2+2k+3\right)⋮3\)
=>p^2+8 không là số nguyên tố
=>Loại
TH4: p=3k+2
\(p^2+8=\left(3k+2\right)^2+8\)
\(=9k^2+12k+4+8=9k^2+12k+12=3\left(3k^2+4k+4\right)⋮3\)
=>p^2+8 không là số nguyên tố
=>Loại
Vậy: p=3

\(-\dfrac{5}{7}\cdot\dfrac{2}{11}+\left(-\dfrac{5}{7}\right)\cdot\dfrac{4}{11}+\dfrac{5}{7}\cdot\left(-\dfrac{5}{11}\right)\\ =-\dfrac{5}{7}\cdot\dfrac{2}{11}+\left(-\dfrac{5}{7}\right)\cdot\dfrac{4}{11}+\left(-\dfrac{5}{7}\right)\cdot\dfrac{5}{11}\\ =\left(-\dfrac{5}{7}\right)\cdot\left(\dfrac{2}{11}+\dfrac{4}{11}+\dfrac{5}{11}\right)\\ =\left(-\dfrac{5}{7}\right)\cdot1=-\dfrac{5}{7}\)

\(\dfrac{5}{7}\cdot\dfrac{6}{13}-\left(-\dfrac{7}{13}\cdot\dfrac{5}{7}\right)+\dfrac{1}{7}:\dfrac{1}{2}\\ =\dfrac{5}{7}\cdot\dfrac{6}{13}-\left(-\dfrac{7}{13}\cdot\dfrac{5}{7}\right)+\dfrac{1}{7}\cdot2\\ =\dfrac{5}{7}\cdot\left[\dfrac{6}{13}-\left(-\dfrac{7}{13}\right)\right]+\dfrac{2}{7}\\ =\dfrac{5}{7}\cdot1+\dfrac{2}{7}=1\)

\(\left(2\dfrac{2}{15}\cdot\dfrac{9}{17}\cdot\dfrac{3}{32}\right):\left(-\dfrac{3}{17}\right)\\ =\left(\dfrac{32}{15}\cdot\dfrac{9}{17}\cdot\dfrac{3}{32}\right)\cdot\left(-\dfrac{17}{3}\right)\\ =\dfrac{32}{15}\cdot\dfrac{9}{17}\cdot\dfrac{3}{32}\cdot\dfrac{-17}{3}\\ =\left(\dfrac{32}{15}\cdot\dfrac{3}{32}\right)\cdot\left(\dfrac{9}{17}\cdot\dfrac{-17}{3}\right)\\ =\dfrac{1}{5}\cdot\left(-3\right)=-\dfrac{3}{5}\)

a)
\(\dfrac{-5}{11}\cdot\dfrac{7}{15}\cdot\dfrac{11}{-5}\cdot\left(-30\right)\\ =\left(\dfrac{-5}{11}\cdot\dfrac{11}{-5}\right)\cdot\left(\dfrac{7}{15}\cdot-30\right)\\ =1\cdot-14\\ =-14\)
b)
\(-\dfrac{1}{3}\cdot\left(-\dfrac{15}{19}\right)\cdot\dfrac{38}{45}\\ =-\dfrac{1}{3}\cdot\left(-\dfrac{15}{29}\cdot\dfrac{38}{45}\right)\\ =-\dfrac{1}{3}\cdot\left(-\dfrac{15}{29}\cdot\dfrac{2\cdot19}{3\cdot15}\right)\\ =-\dfrac{1}{3}\cdot-\dfrac{2}{3}\\ =\dfrac{2}{9}\)

\(9\left(x-1\right)^2-\left(x-1\right)^4=0\\ \Rightarrow\left(x-1\right)^2\left[9-\left(x-1\right)^2\right]\\ \Rightarrow\left[{}\begin{matrix}\left(x-1\right)^2=0\\9-\left(x-1\right)^2=0\end{matrix}\right.\\ \Rightarrow\left[{}\begin{matrix}x-1=0\\9=\left(x-1\right)^2\end{matrix}\right.\\ \Rightarrow\left[{}\begin{matrix}x=1\\3^2=x-1\end{matrix}\right.\\ \Rightarrow\left[{}\begin{matrix}x=1\\x-1=3\\x-1=-3\end{matrix}\right.\\ \Rightarrow\left[{}\begin{matrix}x=1\\x=4\\x=-2\end{matrix}\right.\)
________________________
\(\left(2x-3\right)^2+2x=3\\ \Rightarrow\left(2x-3\right)^2+\left(2x-3\right)=0\\ \Rightarrow\left(2x-3\right)\left(2x-3+1\right)=0\\ \Rightarrow\left(2x-3\right)\left(2x-2\right)=0\\ \Rightarrow\left[{}\begin{matrix}2x-3=0\\2x-2=0\end{matrix}\right.\\ \Rightarrow\left[{}\begin{matrix}2x=3\\2x=2\end{matrix}\right.\\ \Rightarrow\left[{}\begin{matrix}x=\dfrac{3}{2}\\x=\dfrac{2}{2}=1\end{matrix}\right.\)

Chào các bạn đã kết bạn với tớ, các bạn có khỏe mạnh không, giờ tớ đang học nè, còn các cậu đang làm gì.
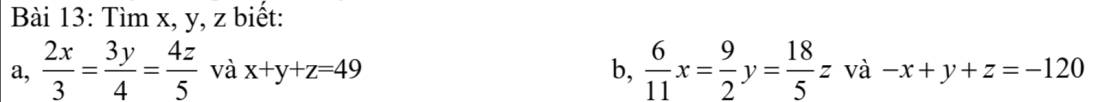
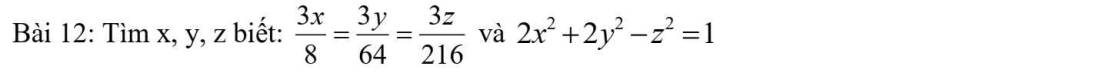
a: Đặt \(\dfrac{a}{2}=\dfrac{b}{3}=\dfrac{c}{4}=k\)
=>a=2k; b=3k; c=4k
\(a^2-b^2+2c^2=108\)
=>\(\left(2k\right)^2-\left(3k\right)^2+2\cdot\left(4k\right)^2=108\)
=>\(4k^2-9k^2+32k^2=108\)
=>\(27k^2=108\)
=>\(k^2=4\)
=>\(\left[{}\begin{matrix}k=2\\k=-2\end{matrix}\right.\)
TH1: k=2
=>\(a=2\cdot2=4;b=3\cdot2=6;c=4\cdot2=8\)
TH2: k=-2
=>\(a=2\cdot\left(-2\right)=-4;b=3\cdot\left(-2\right)=-6;c=4\cdot\left(-2\right)=-8\)
b: Đặt \(\dfrac{x}{3}=\dfrac{y}{4}=\dfrac{z}{5}=k\)
=>x=3k; y=4k; z=5k
\(-3x^2-2y^2+5z^2=594\)
=>\(-3\cdot\left(3k\right)^2-2\cdot\left(4k\right)^2+5\cdot\left(5k\right)^2=594\)
=>\(-27k^2-32k^2+125k^2=594\)
=>\(k^2=9\)
=>\(\left[{}\begin{matrix}k=3\\k=-3\end{matrix}\right.\)
TH1: k=3
=>\(x=3\cdot3=9;y=4\cdot3=12;z=5\cdot3=15\)
TH2: k=-3
=>\(x=3\cdot\left(-3\right)=-9;y=4\cdot\left(-3\right)=-12;z=5\cdot\left(-3\right)=-15\)
a) Đặt: \(\dfrac{a}{2}=\dfrac{b}{3}=\dfrac{c}{4}=k\Rightarrow\left\{{}\begin{matrix}a=2k\\b=3k\\c=4k\end{matrix}\right.\)
\(a^2-b^2+2c^2=108\)
\(\Rightarrow\left(2k\right)^2-\left(3k\right)^2+2\cdot\left(4k\right)^2=108\\ \Rightarrow4k^2-9k^2+32k^2=108\\ \Rightarrow27k^2=108\\ \Rightarrow k^2=4\\ \Rightarrow k=\pm2\)
Với k=2 \(\Rightarrow\left\{{}\begin{matrix}a=2\cdot2=4\\b=3\cdot2=6\\c=4\cdot2=8\end{matrix}\right.\)
Với k=-2 \(\Rightarrow\left\{{}\begin{matrix}a=2\cdot-2=-4\\b=3\cdot-2=-6\\c=4\cdot-2=-8\end{matrix}\right.\)
Vậy: ...
b) \(x:y:z=3:4:5\Rightarrow\dfrac{x}{3}=\dfrac{y}{4}=\dfrac{z}{5}\)
Đặt: \(\dfrac{x}{3}=\dfrac{y}{4}=\dfrac{z}{5}=k\Rightarrow\left\{{}\begin{matrix}x=3k\\y=4k\\z=5k\end{matrix}\right.\)
\(5z^2-3x^2-2y^2=594\\ \Rightarrow5\cdot\left(5k\right)^2-3\cdot\left(3k\right)^2-2\cdot\left(4k\right)^2=594\\ \Rightarrow125k^2-27k^2-32k^2=594\\ \Rightarrow66k^2=594\\ \Rightarrow k^2=\dfrac{594}{66}\\ \Rightarrow k^2=9\\ \Rightarrow k=\pm3\)
Với \(k=3\Rightarrow\left\{{}\begin{matrix}x=3\cdot3=9\\y=4\cdot3=12\\z=5\cdot3=15\end{matrix}\right.\)
Với \(k=-3\Rightarrow\left\{{}\begin{matrix}x=3\cdot-3=-9\\y=4\cdot-3=-12\\z=5\cdot-3=-15\end{matrix}\right.\)
Vậy: ...