Ta có: 

\(P\left(x\right)=x^5-3x^5+7x^4-9x^3+x^3+x^2-\dfrac{1}{4}x\\ =-2x^5+7x^4-8x^3+x^2-\dfrac{1}{4}x\\ =x\cdot\left(-2x^4+7x^3-8x^2+x-\dfrac{1}{4}\right)\)

Thay `x=0` vào P(x) ta có:

\(P\left(x\right)=0\cdot\left(2\cdot0^4+7\cdot0^3-8\cdot0^2+0-\dfrac{1}{4}\right)=0\)

=> `x=0` là nghiệm của P(x) 

\(Q\left(x\right)=5x^4-x^5+x^2-2x^3+3x^2-\dfrac{1}{4}\\ =-x^5+5x^4-2x^3+4x^2-\dfrac{1}{4}\)

Thay `x=0` vào Q(x) ta có: 

\(Q=-0^5+5\cdot0^4-2\cdot0^3+4\cdot0^2-\dfrac{1}{4}=-\dfrac{1}{4}\)

=> `x=0` không phải là nghiệm của Q(x) 

Ta có:

P(0) = 0⁵ - 3⁵ + 7.0⁴ - 9.0³ + 0³ + 0² - 1/4 . 0

= -3⁵

= -243

Vậy x = 0 không là nghiệm của P(x)

Em xem lại đề nhé!

ĐKXĐ: \(x\ne\pm\dfrac{1}{2}\)

\(\dfrac{8x^2}{3\left(1-4x^2\right)}=\dfrac{2x}{6x-3}-\dfrac{1+8x}{4+8x}\)

\(\Leftrightarrow\dfrac{-8x^2}{3\left(2x-1\right)\left(2x+1\right)}=\dfrac{2x}{3\left(2x-1\right)}-\dfrac{1+8x}{4\left(2x+1\right)}\)

\(\Leftrightarrow\dfrac{-32x^2}{12\left(2x-1\right)\left(2x+1\right)}=\dfrac{8x\left(2x+1\right)}{12\left(2x-1\right)\left(2x+1\right)}-\dfrac{3\left(1+8x\right)\left(2x-1\right)}{12\left(2x-1\right)\left(2x+1\right)}\)

\(\Rightarrow-32x^2=16x^2+8x-3\left(16x^2-6x-1\right)\)

\(\Leftrightarrow-32x^2=16x^2+8x-48x^2+18x+3\)

\(\Leftrightarrow-32x^2=-32x^2+26x+3\)

\(\Leftrightarrow26x+3=0\)

\(\Leftrightarrow26x=-3\)

\(\Leftrightarrow x=-\dfrac{3}{26}\) (tmđk)

$Toru$

cảm ơn gì vậy bn

?

2,5+3,2+2,7

=5,7+2,7

=8,4

\(\left[-1,5\right]-\dfrac{1}{5}=-\dfrac{3}{2}-\dfrac{1}{5}=-\dfrac{15}{10}-\dfrac{2}{10}=-\dfrac{17}{10}\)

`#3107.101107`

`2,5 + 3,2 + 2,7`

`= 5,7 + 2,7`

`= 8,4`

____

$-1,5 - \dfrac{1}{5}$

`= -1,5 - 0,2`

`= -1,7`

Ta có: \(\dfrac{y+z+2}{x}=\dfrac{x+z+3}{y}=\dfrac{x+y-5}{z}=\dfrac{1}{x+y+z}\) (\(x,y,z\ne0\))

Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:

\(\dfrac{y+z+2}{x}=\dfrac{x+z+3}{y}=\dfrac{x+y-5}{z}=\dfrac{1}{x+y+z}\)

\(=\dfrac{y+z+2+x+z+3+x+y-5}{x+y+z}=\dfrac{2\left(x+y+z\right)}{x+y+z}=2\)

\(\Rightarrow\left\{{}\begin{matrix}y+z+2=2x\\x+z+3=2y\\x+y-5=2z\\x+y+z=\dfrac{1}{2}\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}x+y+z+2=3x\\x+y+z+3=3y\\x+y+z-5=3z\\x+y+z=\dfrac{1}{2}\end{matrix}\right.\)

\(\Rightarrow\left\{{}\begin{matrix}3x=\dfrac{1}{2}+2=\dfrac{5}{2}\\3y=\dfrac{1}{2}+3=\dfrac{7}{2}\\3z=\dfrac{1}{2}-5=-\dfrac{9}{2}\\x+y+z=\dfrac{1}{2}\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}x=\dfrac{5}{6}\left(tm\right)\\y=\dfrac{7}{6}\left(tm\right)\\z=-\dfrac{3}{2}\left(tm\right)\end{matrix}\right.\)

#$\mathtt{Toru}$

ai giải dc mình tick cho

Bài 7: Kẻ CF//AB//DE(CF,AB cùng nằm trên nửa mặt phẳng bờ AC)

CF//AB

=>\(\widehat{BAC}+\widehat{ACF}=180^0\)

CF//DE

=>\(\widehat{FCD}+\widehat{CDE}=180^0\)

\(\widehat{BAC}+\widehat{ACF}+\widehat{FCD}+\widehat{CDE}\)

\(=180^0+180^0=360^0\)

=>\(\widehat{BAC}+\widehat{ACD}+\widehat{CDE}=360^0\)

Bài 8:

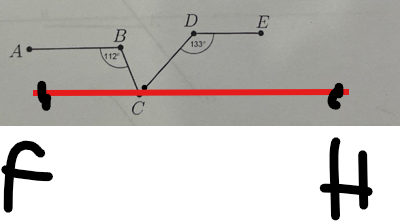
Qua C, kẻ FH//AB//DE

FC//AB

=>\(\widehat{ABC}+\widehat{FCB}=180^0\)

=>\(\widehat{FCB}=68^0\)

Ta có: CH//DE

=>\(\widehat{CDE}+\widehat{DCH}=180^0\)

=>\(\widehat{DCH}=180^0-133^0=47^0\)

Ta có: \(\widehat{BCF}+\widehat{BCD}+\widehat{HCD}=180^0\)

=>\(\widehat{BCD}+47^0+68^0=180^0\)

=>\(\widehat{BCD}=65^0\)

a) Để `x/7` là số hữu tỉ thì \(x\in Z\)

b) Để `5/x` là số hữu tỉ thì \(x\in Z,x\ne0\)

c) Để `-5/(2x)` là số hữu tỉ thì \(2x\in Z\Rightarrow x\in Z,x\ne0\)

\(\dfrac{x}{7}\text{ là số hữu tỉ nếu }x\text{ là số nguyên}\)

\(\dfrac{5}{x}\) là số hữu tỉ nếu x là số nguyên khác 0

\(-\dfrac{5}{2x}\)  là số hữu tỉ nếu x là số nguyên khác 0

*chứng minh AB = AE
xét tam giác vuông ABD và tam giác vuông AED, có: 
góc BAD = góc EAD (vì A là đường phân giác của tam giác ABC)
AD là cạnh chung
=> tam giác ABD = tam giác AED (ch-gn)
=> AB = AE (2 cạnh tương ứng)
*chứng minh DQ = CD
xét tam giác AEQ và tam giác ABC , có:
góc AEQ = góc ABC (= 90 độ)
AB = AE (câu a)
góc A là góc chung
=> tam giác AEQ = tam giác ABC (c-g-c)
=> QE = BC (1)
ta có: DC = BC - BD; DQ = QE - DE (2) 
lại có: DB = DE (vì tam giác ABD = tam giác AED) (3)
=> TỪ (1) (2) (3) => DC = DQ

*chứng minh AB = AE

xét tam giác vuông ABD và tam giác vuông AED, có: 

góc BAD = góc EAD (vì A là đường phân giác của tam giác ABC)

AD là cạnh chung

=> tam giác ABD = tam giác AED (ch-gn)

=> AB = AE (2 cạnh tương ứng)

*chứng minh DQ = CD

xét tam giác AEQ và tam giác ABC , có:

góc AEQ = góc ABC (= 90 độ)

AB = AE (câu a)

góc A là góc chung

=> tam giác AEQ = tam giác ABC (c-g-c)

=> QE = BC (1)

ta có: DC = BC - BD; DQ = QE - DE (2) 

lại có: DB = DE (vì tam giác ABD = tam giác AED) (3)

=> TỪ (1) (2) (3) => DC = DQ