Cho tam giác ABC, I là trung điểm BC. Tìm tập hợp điểm M thỏa mãn \(\mid MA = \mid MB + MC \mid \)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.




2 + 2 = 4 .
Cái này mà là toán lớp 10 à ? .

A. Phương pháp giải & Ví dụ
- Phương trình sinx = a (1)
♦ |a| > 1: phương trình (1) vô nghiệm.
♦ |a| ≤ 1: gọi α là một cung thỏa mãn sinα = a.
Khi đó phương trình (1) có các nghiệm là
x = α + k2π, k ∈ Z
và x = π-α + k2π, k ∈ Z.
Nếu α thỏa mãn điều kiện và sinα = a thì ta viết α = arcsin a.
Khi đó các nghiệm của phương trình (1) là
x = arcsina + k2π, k ∈ Z
và x = π - arcsina + k2π, k ∈ Z.
Các trường hợp đặc biệt:
- Phương trình cosx = a (2)
♦ |a| > 1: phương trình (2) vô nghiệm.
♦ |a| ≤ 1: gọi α là một cung thỏa mãn cosα = a.
Khi đó phương trình (2) có các nghiệm là
x = α + k2π, k ∈ Z
và x = -α + k2π, k ∈ Z.
Nếu α thỏa mãn điều kiện và cosα = a thì ta viết α = arccos a.
Khi đó các nghiệm của phương trình (2) là
x = arccosa + k2π, k ∈ Z
và x = -arccosa + k2π, k ∈ Z.
Các trường hợp đặc biệt:
- Phương trình tanx = a (3)
Điều kiện:
Nếu α thỏa mãn điều kiện và tanα = a thì ta viết α = arctan a.
Khi đó các nghiệm của phương trình (3) là
x = arctana + kπ,k ∈ Z
- Phương trình cotx = a (4)
Điều kiện: x ≠ kπ, k ∈ Z.
Nếu α thỏa mãn điều kiện và cotα = a thì ta viết α = arccot a.
Khi đó các nghiệm của phương trình (4) là
x = arccota + kπ, k ∈ Z
Ví dụ minh họa
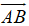
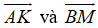
 giải giúp mình bài này , mình đang cần gấp ạ
giải giúp mình bài này , mình đang cần gấp ạ