Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(\text{Δ}=\left[-\left(m+1\right)\right]^2-4\cdot1\cdot\left(-3\right)=\left(m+1\right)^2+12>=12>0\forall x\)
=>Phương trình luôn có hai nghiệm phân biệt
Theo Vi-et, ta có:
\(\left\{{}\begin{matrix}x_1+x_2=-\dfrac{b}{a}=m+1\\x_1x_2=\dfrac{c}{a}=-3\end{matrix}\right.\)
Theo đề, ta có hệ phương trình:
\(\left\{{}\begin{matrix}x_1+x_2=m+1\\x_1-x_2=4\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}2x_1=m+1+4=m+5\\x_1-x_2=4\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x_1=0,5m+2,5\\x_2=x_1-4=0,5m+2,5-4=0,5m-1,5\end{matrix}\right.\)
\(x_1x_2=-3\)
=>\(\left(0,5m+2,5\right)\left(0,5m-1,5\right)=-3\)
=>\(0,25m^2-0,75m+1,25m-3,75+3=0\)
=>\(0,25m^2+0,5m-0,75=0\)
=>\(\left[{}\begin{matrix}m=1\\m=-3\end{matrix}\right.\)
\(ac=-3< 0\Rightarrow\) pt luôn có 2 nghiệm trái dấu với mọi m
Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=m+1\\x_1x_2=-3\end{matrix}\right.\)
Kết hợp với điều kiện đề bài ta được:
\(\left\{{}\begin{matrix}x_1+x_2=m+1\\x_1-x_2=4\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x_1=\dfrac{m+5}{2}\\x_2=\dfrac{m-3}{2}\end{matrix}\right.\)
Thay vào \(x_1x_2=-3\)
\(\left(\dfrac{m+5}{2}\right)\left(\dfrac{m-3}{2}\right)=-3\)
\(\Rightarrow...\) (em tự giải pt bậc 2 ra m)

Số tiền khách hàng phải trả cho mỗi món hàng là:
\(50000.\left(100\%-15\%\right)=42500\) (đồng)
Số tiền khách hàng phải trả cho mỗi món hàng từ thứ 5 trở đi là:
\(42500.70\%=29750\) (đồng)
a.
Số tiền cô Mai phải trả là:
\(4.42500+6.29750=348500\) (đồng)
b.
Do chị Lan trả nhiều tiền hơn cô Mai nên chị Lan mua nhiều hơn cô Mai \(\Rightarrow\) chị Lan mua nhiều hơn 10 món hàng
Gọi x là số món hàng chị Lan đã mua (với \(x>10\)), số tiền chị Lan phải trả là:
\(\left[4.42500+\left(x-4\right).29750\right].80\%\)
Do chị Lan trả tổng cộng 397800 đồng nên ta có pt:
\(\left[4.42500+\left(x-4\right).29750\right].80\%=397800\)
\(\Rightarrow x-4=11\)
\(\Rightarrow x=15\)

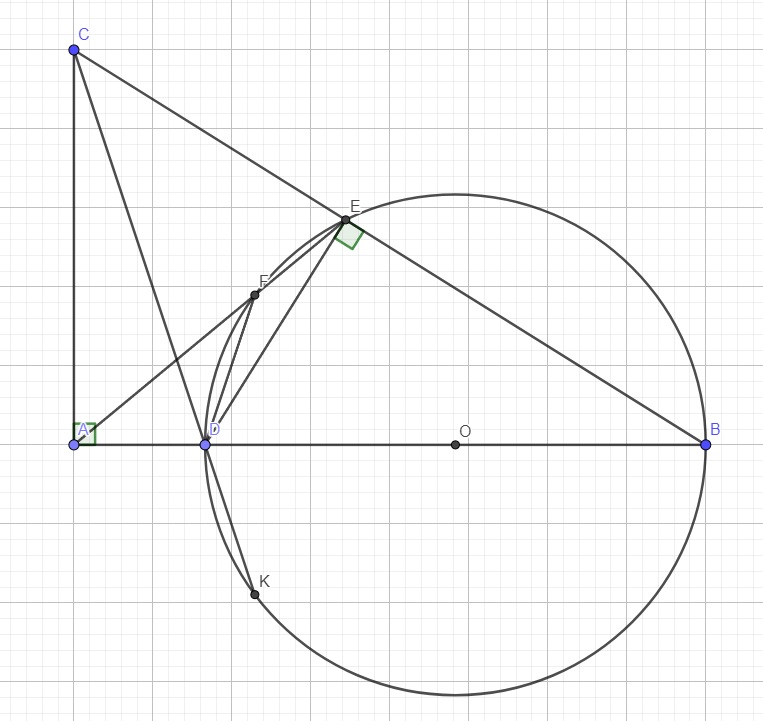
Tứ giác DBEF nội tiếp (O) nên \(\widehat{DBE}+\widehat{DFE}=180^0\)
Mà \(\widehat{DFE}+\widehat{DFA}=180^0\) (kề bù)
\(\Rightarrow\widehat{DFA}=\widehat{DBE}\)
Xét 2 tam giác ADF và AEB có:
\(\left\{{}\begin{matrix}\widehat{DAF}-chung\\\widehat{DFA}=\widehat{DBE}\left(cmt\right)\end{matrix}\right.\)
\(\Rightarrow\Delta ADF\sim\Delta AEB\left(g.g\right)\)
\(\Rightarrow\dfrac{AF}{AB}=\dfrac{AD}{AE}\Rightarrow AE.AF=AD.AB\) (1)
Do BD là đường kính của (O) \(\Rightarrow\widehat{BED}=90^0\) (góc nt chắn nửa đường tròn)
Xét 2 tam giác BED và BAC có:
\(\left\{{}\begin{matrix}\widehat{B}-chung\\\widehat{BED}=\widehat{BAC}=90^0\end{matrix}\right.\)
\(\Rightarrow\Delta BED\sim\Delta BAC\left(g.g\right)\)
\(\Rightarrow\dfrac{BE}{AB}=\dfrac{BD}{BC}\Rightarrow BE.BC=AB.BD\) (2)
Từ (1); (2):
\(\Rightarrow AE.AF+BE.BC=AD.AB+AB.BD=AB\left(AD+BD\right)=AB^2\) (không đổi)


a: Khi m=2 thì (d): \(y=2\cdot x+2^2+4=2x+8\)
Phương trình hoành độ giao điểm là:
\(x^2=2x+8\)
=>\(x^2-2x-8=0\)
=>(x-4)(x+2)=0
=>\(\left[{}\begin{matrix}x=4\\x=-2\end{matrix}\right.\)
Khi x=4 thì \(y=4^2=16\)
Khi x=-2 thì \(y=\left(-2\right)^2=4\)
Vậy: (d) cắt (P) tại A(4;16); B(-2;4)
b: Phương trình hoành độ giao điểm là:
\(x^2=mx+m^2+4\)
=>\(x^2-mx-m^2-4=0\)
\(a\cdot c=1\cdot\left(-m^2-4\right)=-m^2-4< =-4< 0\forall m\)
=>(P) luôn cắt (d) tại hai điểm phân biệt nằm ở hai phía của trục tung
A nằm bên trái trục tung nên x1<0
B nằm bên phải trục tung nên x2>0
Theo Vi-et, ta có:
\(\left\{{}\begin{matrix}x_1+x_2=-\dfrac{b}{a}=m\\x_1x_2=\dfrac{c}{a}=-m^2-4\end{matrix}\right.\)
\(\left|x_1\right|-\left|x_2\right|=3\)
=>\(\left(\left|x_1\right|-\left|x_2\right|\right)^2=3^2=9\)
=>\(x_1^2+x_2^2-2\left|x_1x_2\right|=9\)
=>\(\left(x_1+x_2\right)^2-2x_1x_2-2\left|x_1x_2\right|=9\)
=>\(m^2-2\left(-m^2-4\right)-2\left|-m^2-4\right|=9\)
=>\(m^2+2\left(m^2+4\right)-2\left(m^2+4\right)=9\)
=>\(m^2=9\)
=>\(\left[{}\begin{matrix}m=3\\m=-3\end{matrix}\right.\)

Ta có: \(\left(x+y+z\right)^2=x^2+y^2+z^2\)
\(\Leftrightarrow x^2+y^2+z^2+2xy+2yz+2zx-x^2-y^2-z^2=0\)
\(\Leftrightarrow2\left(xy+yz+zx\right)=0\)
\(\Leftrightarrow xy+yz+zx=0\)
Đặt \(\dfrac{1}{x}=a;\dfrac{1}{y}=b;\dfrac{1}{z}=c\Rightarrow\dfrac{3}{xyz}=3abc\)
Lại có: \(xy+yz+zx=0\Rightarrow\dfrac{1}{ab}+\dfrac{1}{bc}+\dfrac{1}{ca}=0\)
\(\Leftrightarrow\dfrac{a+b+c}{abc}=0\Leftrightarrow a+b+c=0\)
Khi đó, xét hiệu: \(\dfrac{1}{x^3}+\dfrac{1}{y^3}+\dfrac{1}{z^3}-\dfrac{3}{xyz}\)
\(=a^3+b^3+c^3-3abc\)
\(=\left(a+b\right)^3+c^3-3ab\left(a+b\right)-3abc\)
\(=\left(a+b+c\right)^3-3\left(a+b\right)c\left(a+b+c\right)-3ab\left(a+b+c\right)\)
\(=0\) (do \(a+b+c=0\))
\(\Rightarrow\dfrac{1}{x^3}+\dfrac{1}{y^3}+\dfrac{1}{z^3}=\dfrac{3}{xyz}\) (đpcm)
\(Toru\)

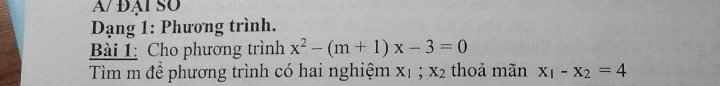
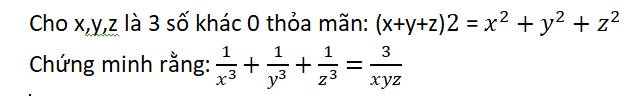
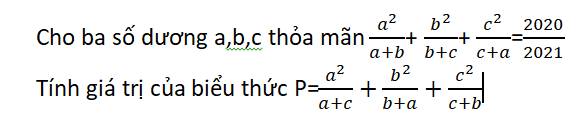
Áp dụng Bunhiacopxki:
\(\left(a+1\right)^2=\left(\sqrt{ab}.\sqrt{\dfrac{a}{b}}+1.1\right)^2\le\left(ab+1\right)\left(\dfrac{a}{b}+1\right)=\dfrac{\left(ab+1\right)\left(a+b\right)}{b}\)
\(\Rightarrow\dfrac{1}{\left(a+1\right)^2}\ge\dfrac{b}{\left(ab+1\right)\left(a+b\right)}\)
Tương tự: \(\dfrac{1}{\left(b+1\right)^2}\ge\dfrac{a}{\left(ab+1\right)\left(a+b\right)}\)
\(\Rightarrow\dfrac{1}{\left(a+1\right)^2}+\dfrac{1}{\left(b+1\right)^2}\ge\dfrac{b}{\left(ab+1\right)\left(a+b\right)}+\dfrac{a}{\left(ab+1\right)\left(a+b\right)}=\dfrac{1}{ab+1}\)
Mà \(abc=1\Rightarrow ab=\dfrac{1}{c}\)
\(\Rightarrow\dfrac{1}{\left(a+1\right)^2}+\dfrac{1}{\left(b+1\right)^2}\ge\dfrac{1}{\dfrac{1}{c}+1}=\dfrac{c}{c+1}\)
Theo nguyên lý Dirichlet, trong 3 số a;b;c luôn có ít nhất 2 số cùng phía so với 1. Không mất tính tổng quát, giả sử đó là a và b
\(\Rightarrow\left(a-1\right)\left(b-1\right)\ge0\)
\(\Rightarrow ab+1\ge a+b\)
\(\Rightarrow2ab+2\ge ab+a+b+1=\left(a+1\right)\left(b+1\right)\)
\(\Rightarrow\dfrac{2}{\left(a+1\right)\left(b+1\right)}\ge\dfrac{1}{ab+1}\)
\(\Rightarrow\dfrac{2}{\left(a+1\right)\left(b+1\right)\left(c+1\right)}\ge\dfrac{1}{\left(ab+1\right)\left(c+1\right)}=\dfrac{1}{\left(\dfrac{1}{c}+1\right)\left(c+1\right)}=\dfrac{c}{\left(c+1\right)^2}\)
Gọi vế trái BĐT cần c/m là P
\(\Rightarrow P\ge\dfrac{c}{c+1}+\dfrac{1}{\left(c+1\right)^2}+\dfrac{c}{\left(c+1\right)^2}=1\) (đpcm)
Dấu "=" xảy ra khi \(a=b=c=1\)