cho các số thực dương a,b,c thoa man 1/a+1 + 1/b+1 +1/c+1<=1 tìm GTNN của P= a^3/a^2+ab+b^2 + b^3/b^2+bc+c^2 + c^3/c^2+ca+a^2 . Mọi người giải giúp mình bài bđt này với ạ
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


ĐKXĐ: \(x\ne0;y\ne0\)
y-x=6
=>y=x+6
\(\dfrac{12}{x}-\dfrac{12}{y}=\dfrac{1}{10}\)
=>\(\dfrac{12}{x}-\dfrac{12}{x+6}=\dfrac{1}{10}\)
=>\(\dfrac{12\left(x+6\right)-12x}{x\left(x+6\right)}=\dfrac{1}{10}\)
=>\(\dfrac{72}{x\left(x+6\right)}=\dfrac{1}{10}\)
=>\(x\left(x+6\right)=720\)
=>\(x^2+6x-720=0\)
=>\(x^2+6x+9=729\)
=>\(\left(x+3\right)^2=729\)
=>\(\left[{}\begin{matrix}x+3=27\\x+3=-27\end{matrix}\right.\)
=>\(\left[{}\begin{matrix}x=24\left(nhận\right)\\x=-30\left(nhận\right)\end{matrix}\right.\)
Khi x=24 thì \(y=x+6=24+6=30\left(nhận\right)\)
Khi x=-30 thì \(y=x+6=-30+6=-24\left(nhận\right)\)

Để A là số nguyên dương thì \(\left\{{}\begin{matrix}\sqrt{x}⋮\sqrt{x}+3\\A>0\end{matrix}\right.\)
=>\(\sqrt{x}+3-3⋮\sqrt{x}+3\)
=>\(-3⋮\sqrt{x}+3\)
=>\(\sqrt{x}+3\in\left\{1;-1;3;-3\right\}\)
=>\(\sqrt{x}+3=3\)
=>x=0(loại)
vậy: Không có giá trị nào của x để A là số nguyên dương

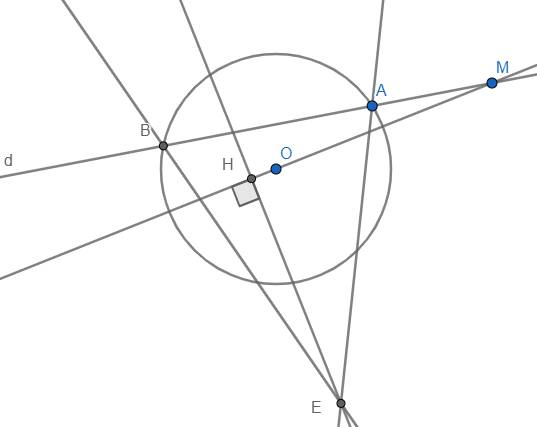
a: Xét (O) có
ΔADB nội tiếp
AB là đường kính
Do đó: ΔADB vuông tại D
Xét tứ giác ADEH có \(\widehat{ADE}+\widehat{AHE}=90^0+90^0=180^0\)
nên ADEH là tứ giác nội tiếp

Để K là số nguyên dương thì \(\left\{{}\begin{matrix}\sqrt{x}⋮\sqrt{x}-3\\K>0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}\sqrt{x}-3+3⋮\sqrt{x}-3\\\sqrt{x}-3>0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}3⋮\sqrt{x}-3\\\sqrt{x}-3>0\end{matrix}\right.\)
=>\(\sqrt{x}-3\in\left\{1;3\right\}\)
=>\(\sqrt{x}\in\left\{4;6\right\}\)
=>\(x\in\left\{16;36\right\}\)

Gọi vận tốc của Thành là x(km/h)
(Điều kiện: x>0)
Vận tốc của Công là x+6(km/h)
Thời gian Thành đi là \(\dfrac{12}{x}\left(giờ\right)\)
Thời gian Công đi là \(\dfrac{12}{x+6}\left(giờ\right)\)
Công đến trước Thành 6p=0,1 giờ nên ta có:
\(\dfrac{12}{x}-\dfrac{12}{x+6}=0,1\)
=>\(\dfrac{12\left(x+6\right)-12x}{x\left(x+6\right)}=0,1\)
=>x(x+6)=720
=>\(x^2+6x-720=0\)
=>\(\left(x+30\right)\left(x-24\right)=0\)
=>\(\left[{}\begin{matrix}x=-30\left(nhận\right)\\x=24\left(nhận\right)\end{matrix}\right.\)
vậy: Vận tốc của Thành là 24km/h
Vận tốc của CÔng là 24+6=30km/h

Để P là số nguyên thì \(-2⋮\sqrt{x}+1\)
=>\(\sqrt{x}+1\in\left\{1;-1;2;-2\right\}\)
=>\(\sqrt{x}\in\left\{0;-2;1;-3\right\}\)
=>\(\sqrt{x}\in\left\{0;1\right\}\)
=>\(x\in\left\{0;1\right\}\)
Kết hợp ĐKXĐ, ta được: \(x\in\varnothing\)
=>Không có giá trị x nào để P nguyên
\(\left\{{}\begin{matrix}-2< 0\\\sqrt{x}+1>0\end{matrix}\right.\) \(\Rightarrow\dfrac{-2}{\sqrt{x}+1}< 0\Rightarrow P< 0\)
\(\sqrt{x}+1>1;\forall x>0\Rightarrow\dfrac{2}{\sqrt{x}+1}< 2\Rightarrow\dfrac{-2}{\sqrt{x}+1}>-2\)
\(\Rightarrow-2< P< 0\)
Mà P nguyên \(\Rightarrow P=-1\Rightarrow\dfrac{-2}{\sqrt{x}+1}=-1\)
\(\Rightarrow\sqrt{x}+1=2\Rightarrow x=1\) (ko thỏa mãn ĐKXĐ)
Vậy ko tồn tại x để P nguyên

Gọi số than đội xe phải chở mỗi ngày theo kế hoạch là x (tấn)
Thời gian chở hết than theo kế hoạch là: \(\dfrac{120}{x}\) ngày
Thực tế mỗi ngày đội chở được: \(x+6\) tấn
Thực tế số than đội chở được là: \(120+10=130\) (tấn)
Thực tế thời gian chở hết số than là: \(\dfrac{130}{x+6}\) ngày
Do đội hoàn thành trước kế hoạch 1 ngày nên ta có pt:
\(\dfrac{120}{x}-\dfrac{130}{x+6}=1\)
\(\Rightarrow120\left(x+6\right)-130x=x\left(x+6\right)\)
\(\Leftrightarrow x^2+16x-720=0\Rightarrow\left[{}\begin{matrix}x=20\\x=-36\left(loại\right)\end{matrix}\right.\)

\(C=3+2\sqrt{4x^2-8x+13}\)
\(=3+2\sqrt{4x^2-8x+4+9}\)
\(=3+2\sqrt{\left(2x-2\right)^2+9}>=3+2\cdot\sqrt{9}=9\)
Dấu '=' xảy ra khi 2x-2=0
=>x=1
\(D=\left(\sqrt{x}-6\right)^2+\left(\sqrt{x}+2\right)^2\)
\(=x-12\sqrt{x}+36+x+4\sqrt{x}+4\)
\(=2x-8\sqrt{x}+40\)
\(=2\left(x-4\sqrt{x}+20\right)\)
\(=2\left(x-4\sqrt{x}+4+16\right)\)
\(=2\left(\sqrt{x}-2\right)^2+32>=32\forall x\) thỏa mãn ĐKXĐ
Dấu '=' xảy ra khi \(\sqrt{x}-2=0\)
=>x=4
\(F=x+y-2\sqrt{x+2}-4\sqrt{y-1}+10\)
\(=x+2-2\sqrt{x+2}+1+y-1-4\sqrt{y-1}+4+4\)
\(=\left(\sqrt{x+2}-1\right)^2+\left(\sqrt{y-1}-2\right)^2+4>=4\forall x,y\) thỏa mãn ĐKXĐ
Dấu '=' xảy ra khi \(\left\{{}\begin{matrix}x+2=1\\y-1=4\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=-1\\y=5\end{matrix}\right.\)

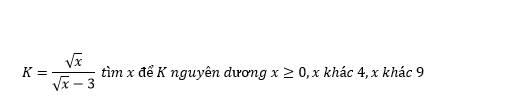

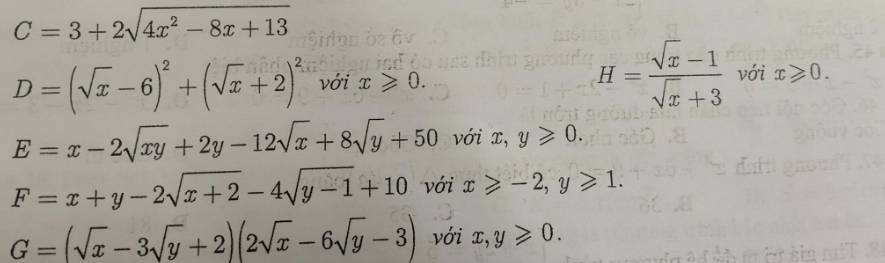
\(1\ge\dfrac{1}{a+1}+\dfrac{1}{b+1}+\dfrac{1}{c+1}\ge\dfrac{9}{a+1+b+1+c+1}\)
\(\Rightarrow a+b+c+3\ge9\Rightarrow a+b+c\ge6\)
Ta có:
\(\dfrac{a^3}{a^2+ab+b^2}=\dfrac{a\left(a^2+ab+b^2\right)-a\left(ab+b^2\right)}{a^2+ab+b^2}\)
\(=a-\dfrac{ab\left(a+b\right)}{a^2+ab+b^2}\ge a-\dfrac{ab\left(a+b\right)}{3\sqrt[3]{a^2.ab.b^2}}=a-\dfrac{a+b}{3}=\dfrac{2a}{3}-\dfrac{b}{3}\)
Tương tự: \(\dfrac{b^3}{b^2+bc+c^2}\ge\dfrac{2b}{3}-\dfrac{c}{3}\)
\(\dfrac{c^3}{c^2+ca+a^2}\ge\dfrac{2c}{3}-\dfrac{a}{3}\)
Cộng vế:
\(\dfrac{a^3}{a^2+ab+b^2}+\dfrac{b^3}{b^2+bc+c^2}+\dfrac{c^3}{c^2+ca+a^2}\ge\dfrac{a+b+c}{3}\ge\dfrac{6}{3}=2\)
Dấu "=" xảy ra khi \(a=b=c=2\)