Lời giải của bạn Trương Nhật Minh:
Để tổng cặp tam giác đối diện chứa số 1 thõa mãn bài toán thì tam giác đối diện tam giác chứa số 1 phải chứa số 4 hoặc 6.
Ta xét các trường hợp sau:
- Tam giác đối diện tam giác số 1 chứa số 4:
2 cặp tam giác đối diện còn lại chứa các cặp số (6;3); (5;2)
Có 2 cách sắp xếp 2 cặp số này vào 2 cặp tam giác đối diện.
Mỗi cặp số có 2 cách sắp xếp 2 số vào 2 tam giác đối diện
Số cách sắp xếp 2 cặp số vào 2 cặp tam giác đối diện là: 2.2.2 = 8 (Cách)
- Tam giác đối diện số 1 chứa số 6
Khi đó 2 cặp tam giác đối diện chứa các cặp số (2;3); (4;5) hoặc (2;5); (3;4)
Số cách sắp xếp các số trong trường hợp này là: 8 + 8 = 16 (cách)
Vậy tổng số cách đặt các số vào các tam giác thõa mãn bài toán là: 8 + 16 = 24 (cách)
Trong hình lục giác dưới đây, số $1$ được đặt vào tam giác trên cùng. Hỏi có bao nhiêu cách khác nhau để đặt các số $2$, $3$, $4$, $5$ và $6$ vào các tam giác trống còn lại, sao cho tổng các số trong các tam giác đối diện nhau là $5$, $7$ hoặc $9$?
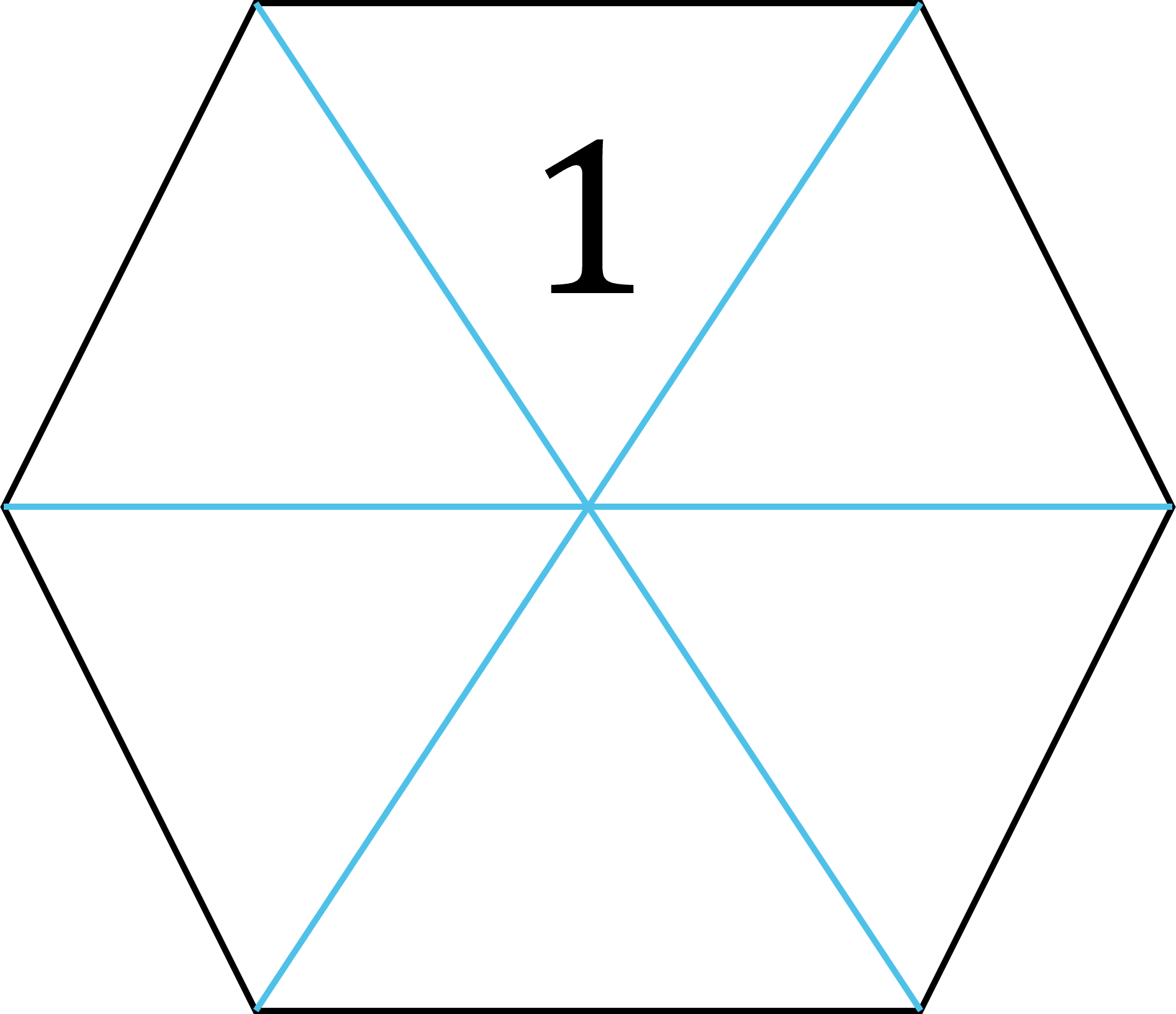
------------------------
Các bạn nhấn vào nút 'Gửi bài làm' bên dưới để trình bày lời giải đầy đủ của mình. Mười bạn có lời giải hay và sớm nhất sẽ được cộng/thưởng coin của OLM để đổi ra tiền mặt, thẻ cào, ngày VIP,... Giải thưởng sẽ được công bố vào Thứ Sáu ngày 24/03/2023. Câu đố tiếp theo sẽ lên mạng vào Thứ Sáu ngày 24/03/2023.
