Giá trị của tham số $m$ để hai mặt phẳng $(P):\,mx+(2m+3 )y-2z+5=0$ và $(Q):\,x-y+2z-1=0$ song song với nhau là

Trong không gian $Oxyz$, cho mặt phẳng $(P)$: $3x+2y-z-1=0$. Vectơ nào dưới đây không phải một vectơ pháp tuyến của mặt phẳng $(P )$?

Trong không gian với hệ tọa độ $Oxyz,$ cho hai đường thẳng $d_1: \dfrac{x-3}{-2}=\dfrac{y-1}{4}=\dfrac{z}{-6}.$ và $d_2:\dfrac{x}{1}=\dfrac{y+1}{-2}=\dfrac{z-5}{3}.$ Vị trí tương đối của $d_1$ và $d_2$ là

Trong không gian với hệ tọa độ $Oxyz$, cho hai đường thẳng $d:\left\{ \begin{aligned}&x=1-t \\&y=2+2t \\&z=3t \end{aligned} \right.$ và $\Delta:\left\{ \begin{aligned} &x=1+t' \\&y=3-2t' \\&z=1 \end{aligned} \right.$. Vị trí tương đối của hai đường thẳng là

Trong không gian ${ O x y z}$, mặt cầu $\left( S \right):{{\left( x-2 \right)}^{2}}+{{\left( y-1 \right)}^{2}}+{{\left( z+3 \right)}^{2}}=16$ đi qua điểm nào dưới đây?

Trong hệ toạ độ $Oxyz$, mặt cầu $\left( S \right):{{x}^{2}}+{{y}^{2}}+{{\left( z-3 \right)}^{2}}=1$ có tâm là điểm nào dưới đây?

Trong không gian hệ tọa độ $Oxyz$, cho ba điểm $A(1;\,-1;\,-1)$, $B(1;\,0;\,4)$, $C(0;\,-2;\,-1)$. Phương trình mặt phẳng $(\alpha)$ qua $A$ và vuông góc với đường thẳng $BC$ là

Trong không gian $Oxyz$, cho đường thẳng $d: \, \left\{ \begin{aligned}& x=t \\& y=1-t \\& z=2 \\ \end{aligned} \right. \, (t \in \mathbb{R})$. Mặt phẳng đi qua $O$ và chứa $d$ có phương trình là

Trong không gian với hệ tọa độ $Oxyz$, cho hình chóp $S.ABCD$ có đáy là hình thang vuông tại $A$ và $B$ có các đỉnh lần lượt là $S(0;0;2a)$; $A(0; 0; 0)$; $B(a; 0; 0)$; $C(a;a;0)$; $D(0; 2a; 0)$, với $a>0$.

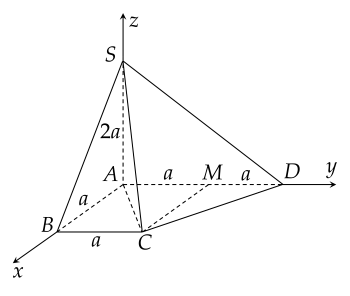
Góc giữa đường thẳng $SD$ và mặt phẳng $(SAC)$ bằng

Tìm tâm và bán kính mặt cầu có phương trình sau:

$x^2 + y^2 + z^2+4x-6z+12=0$

Trong không gian với hệ tọa độ $Oxyz$, cho ba điểm $A(2;3;-1),\,B(4;1;0),\,C(4;7;3)$.

Trong hệ trục tọa độ cho các điểm $M(0;\,2;\,0 ),\,N(0;\,0;\,-1 ),\,P(-1;\,0;\,3 )$.

Trong không gian $Oxyz$, cho đường thẳng $\Delta:\dfrac{x-1}{3}=\dfrac{y-1}{4}=\dfrac{z}{5}$ và hai mặt phẳng $(\alpha ):\ -x+2y-2z+1=0$, $(\beta ):\ 2x+my+mz-1=0$.

Trong không gian với hệ tọa độ $Oxyz$ (đơn vị trên mỗi trục là kilômét), một trạm thu phát sóng điện thoại di động được đặt ở vị trí $I(-1; 2; 5)$. Biết trạm thu phát sóng đó được thiết kế với bán kính phủ sóng là $4$ km.