Cho $a$ là số thực dương. Viết biểu thức $P={{a}^{2}}.{{a}^{\frac{2}{5}}}$ dưới dạng lũy thừa mũ hữu tỉ cơ số $a$ ta được kết quả là

Cho hình chóp $S.ABC$ có $SA\bot \Big(ABC \Big),$ tam giác $ABC$ vuông tại $B$. Kết luận nào sau đây sai?

Cho hình chóp $S.ABC$ có đáy $ABC$ là tam giác vuông cân tại $B$, cạnh bên $SA$ vuông góc với đáy.

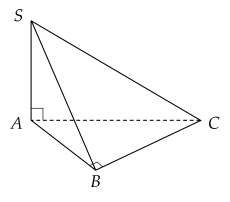
Số đo của góc nhị diện $\left[ B,SA,C \right]$ bằng

Một học sinh tô ngẫu nhiên $5$ câu trắc nghiệm (mỗi câu có $4$ phương án lựa chọn, trong đó chỉ có $1$ phương án đúng). Xác suất để học sinh đó tô sai cả $5$ câu bằng

Đường cong trong hình vẽ là của đồ thị hàm số nào sau đây?

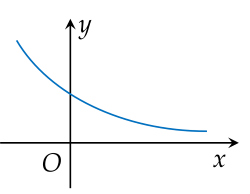
Cho hình chóp $S.ABCD$, có đáy $ABCD$ là hình vuông cạnh $a$, $SA\bot \Big(ABCD \Big)$ và $SA=\dfrac{a\sqrt{3}}{3}$. Khoảng cách từ điểm $A$ đến mặt phẳng $\Big(SCD \Big)$ là

Cho hàm số $y=f\big(x \big)$ xác định trên $\mathbb{R}$ và có ${f}'\Big(2 \Big)=5$. Phương trình tiếp tuyến của đồ thị hàm số $y=f\big(x \big)$ tại $M\Big(2;1 \Big)$ là

Hai người cùng bắn độc lập vào một mục tiêu. Xác suất bắn trúng của từng người lần lượt là $0,8$ và $0,9$. Xác suất của biến cố $A$: “ Chỉ có một người bắn trúng mục tiêu ” là

Cho hàm số $y=\Big(x+2 \Big)^{-2}$. Hệ thức liên hệ giữa $y$ và $y''$ không phụ thuộc vào $x$ là

Cho phương trình ${{4}^{{{x}^{2}}+1}}-{{2}^{2{{x}^{2}}+1}}+m>0$. Xét tính đúng sai của các mệnh đề sau:

Cho hàm số $y={{x}^{3}}+1$ có đồ thị $\Big(C \Big)$.

Một hộp đựng 9 tấm thẻ cùng loại được đánh số từ 1 đến 9. Rút ngẫu nhiên đồng thời hai tấm thẻ từ hộp. Xét các biến cố sau:

$A$: “Cả hai tấm thẻ đều ghi số chẵn”.

$B$: “Chỉ có một tấm thẻ ghi số chẵn”.

$C$: “Tích hai số ghi trên hai tấm thẻ là một số chẵn”.

$D$: “Tổng hai số ghi trên hai tấm thẻ là một số chẵn”.

Cho hình chóp $S.ABC$ có $ABC$ là tam giác đều cạnh $a$ và cạnh bên $SA$ vuông góc với đáy, với $SA=\dfrac{a}{2}$.