Bài học cùng chủ đề
Báo cáo học liệu
Mua học liệu
Mua học liệu:
-
Số dư ví của bạn: 0 coin - 0 Xu
-
Nếu mua học liệu này bạn sẽ bị trừ: 0 coin\Xu
Để nhận Coin\Xu, bạn có thể:

Đề kiểm tra giữa học kì I (đề số 1) SVIP
Yêu cầu đăng nhập!
Bạn chưa đăng nhập. Hãy đăng nhập để làm bài thi tại đây!
Cho hàm số y=2x2+1. Mệnh đề nào dưới đây sai?
Cho hàm số y=f(x) có bảng biến thiên như sau:
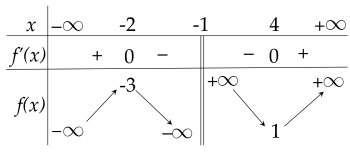
Giá trị cực tiểu của hàm số đã cho bằng
Cho hàm số y=f(x) có bảng biến thiên như sau:
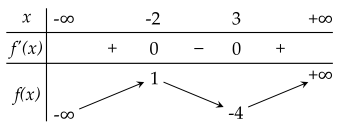
Hàm số đã cho nghịch biến trên khoảng nào dưới đây?
Giá trị nhỏ nhất của hàm số y=f(x)=x4−6x2−1 trên đoạn [−1;3] bằng
Cho đồ thị hàm số y=f(x) có đồ thị như hình vẽ:
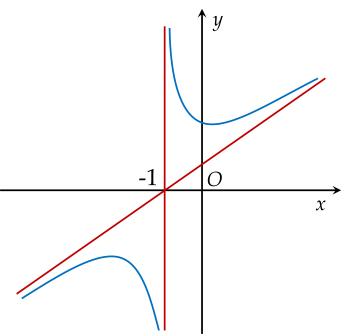
Tiệm cận đứng của đồ thị hàm số là đường thẳng
Đường cong trong hình vẽ là đồ thị của hàm số nào sau đây?
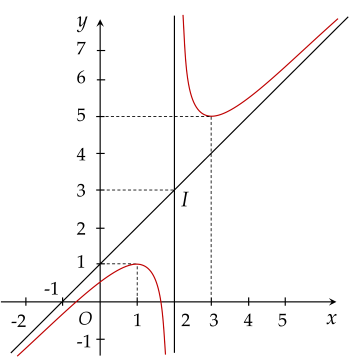
Cho hàm số y=f(x) có đồ thị là đường cong như hình vẽ:
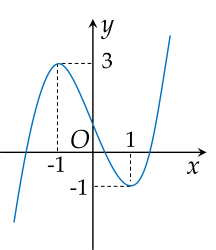
Số nghiệm của phương trình f(x)+2=0 là
Một công ty chuyên sản xuất đồ gia dụng ước tính chi phí để sản xuất x (sản phẩm) là: C(x)=2x+50 (triệu đồng), khi đó G(x)=xC(x) là chi phí sản xuất cho mỗi sản phẩm. Xem G(x) là một hàm số xác định trên [0;+∞), số tiệm cận ngang của đồ thị hàm số G(x) là
Với giá trị nào dưới đây của m thì hàm số y=cos2x+mx đồng biến trên R?
Số giá trị của tham số m để đồ thị hàm số y=mx+1x+m không có tiệm cận đứng là
Cho hàm số y=f(x) liên tục và có đồ thị trên đoạn [−2;4] như hình vẽ.
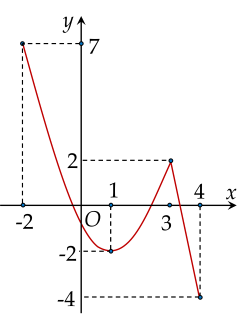
| a) Trên đoạn [−2;4], đồ thị hàm số y=f(x) có 2 điểm cực trị. |
|
| b) Giá trị nhỏ nhất của hàm số y=f(x) trên đoạn [−2;2] là −2. |
|
| c) Giá trị lớn nhất của hàm số y=f(x) trên đoạn [1;4] là −4. |
|
| d) Hiệu giữa giá trị lớn nhất và giá trị nhỏ nhất của hàm số y=f(x) trên đoạn [−2;4] là 11. |
|
Cho hàm số y=f(x) có bảng biến thiên như sau
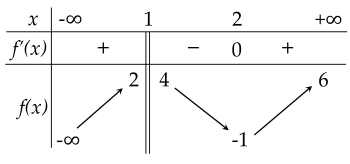
| a) Đồ thị hàm số có đường tiệm cận đứng là x=1. |
|
| b) Đồ thị hàm số có đường tiệm cận ngang là y=6. |
|
| c) Tổng số đường tiệm cận của đồ thị hàm số đã cho là 2. |
|
| d) Tổng số tiệm cận ngang của đồ thị hàm số y=f(x)+21 là 1. |
|
Một loại thuốc được dùng cho một bệnh nhân và nồng độ thuốc trong máu của bệnh nhân được giám sát bởi bác sĩ. Biết rằng nồng độ thuốc trong máu của bệnh nhân sau khi tiêm vào cơ thể trong t giờ được cho bởi hàm số có công thức c(t)=t2+1t (mg/L).
(Nhấp vào ô màu vàng để chọn đúng / sai)| a) Nồng độ thuốc trong máu của bện nhân sau 3 giờ là c(3)=103 (mg/L). |
|
| b) Đạo hàm của hàm số c(t)=t2+1t là c′(t)=(t2+1)21−t2. |
|
| c) Nồng độ thuốc trong máu bệnh nhân tăng trong khoảng t∈(0;2). |
|
| d) Nồng độ thuốc trong máu của bệnh nhân cao nhất khi t=21. |
|
Cho hàm số y=f(x) có bảng biến thiên như sau:
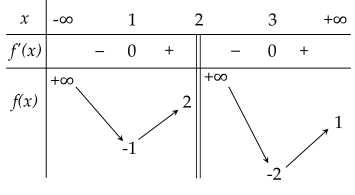
| a) Giá trị nhỏ nhất của hàm số trên [−2,5;1,5] là −2. |
|
| b) Hàm số xác định và liên tục trên R. |
|
| c) Điểm cực tiểu của đồ thị hàm số đã cho là (3;−2). |
|
| d) Với −1<m<1 thì phương trình f(x)=m có 4 nghiệm phân biệt. |
|
Người ta muốn làm một cái bể dạng hình hộp chữ nhật không nắp (như hình vẽ) có thể tích bằng 1 m3. Chiều cao của bể là 5dm, các kích thước khác là x m, y m với x>0 và y>0. Diện tích toàn phần của bể (không kể nắp) là hàm số S(x) trên khoảng (0;+∞).
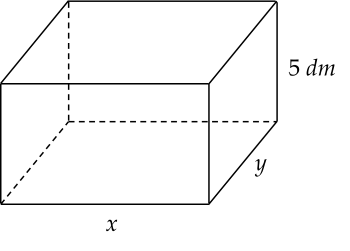
Đường tiệm cận xiên của đồ thị hàm số S(x) là đường thẳng y=ax+b. Tính P=a2+b2.
Trả lời:
Xét một chất điểm chuyển động dọc theo trục Ox. Toạ độ của chất điểm tại thời điểm t được xác định bởi hàm số x(t)=t3−6t2+9t với t≥0. Khi đó x′(t) là vận tốc của chất điểm tại thời điểm t, kí hiệu v(t);v′(t) là gia tốc chuyển động của chất điểm tại thời điểm t. Vận tốc của chất điểm giảm dần tới thời điểm ta lại bắt đầu tăng dần. Tính ta.
Trả lời:
Một chất điểm chuyển động theo quy luật và quãng đường di chuyển được sau t giây được tính theo công thức S(t)=−3t3+243t2 (m). Vận tốc v (m/s) của chuyển động đạt giá trị lớn nhất khi t bằng bao nhiêu giây?
Trả lời:
Một hãng dược phẩm dùng những chiếc lọ bằng nhựa có dạng hình trụ để đựng thuốc. Biết rằng mỗi lọ có thể tích là 16π cm3 và bề dày không đáng kể. Tính bán kính đáy R, đơn vị cm của lọ để tốn ít nguyên liệu sản xuất lọ nhất (kể cả nắp lọ).
Trả lời:
Cho hàm số y=f(x) xác định trên R\{0} và có bảng biến thiên như hình sau:
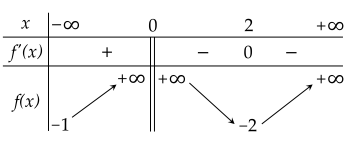
Phương trình f(x2)=1 có bao nhiêu nghiệm?
Trả lời:
Cho hàm số y=f(x) có đạo hàm trên R và thoả mãn f(−3)=f(3)=21. Biết rằng hàm số y=f′(x) là một hàm số bậc ba có đồ thị như hình vẽ.
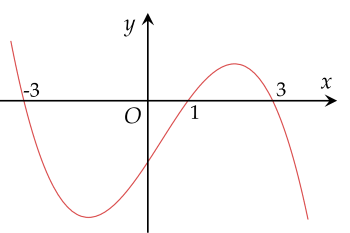
Hàm số g(x)=[f(3−x)]2−f(3−x) đồng biến trên khoảng (a;+∞). Tìm giá trị nguyên nhỏ nhất của a.
Trả lời:
