Đề kiểm tra học kì I (đề số 3)

Câu 1 (1đ):

Cho hàm số $y=f(x)$ có bảng biến thiên như sau:

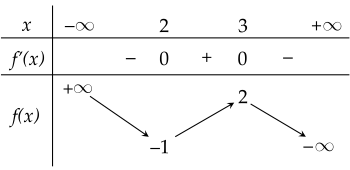
loading...

Khẳng định nào sau đây đúng?

Hàm số đồng biến trên khoảng

\Big(2;\,\dfrac{5}{2} \Big)

.

Hàm số nghịch biến trên khoảng

(-\infty ;\,3)

.

Hàm số nghịch biến trên khoảng

\left(-\infty ;\,2 \right]\cup \left[ 3;\,\,+\infty \right)

.

Hàm số đồng biến trên đoạn

\left[ -1;\,\,2 \right]

.

Câu 2 (1đ):

Số điểm cực trị của hàm số $y=2x^4-4x^2+2 \, 024$ là

4

.

1

.

2

.

3

.

Câu 3 (1đ):

Cho hàm số $y=f\left( x \right)$ có bảng xét dấu đạo hàm như sau.

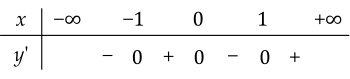
loading...

Mệnh đề nào sau đây đúng?

\underset{\left( -1;\,+\infty \right)}{\mathop{\min }}\,f\left( x \right)=f\left( 0 \right)

.

\underset{\left( 0;\,+\infty \right)}{\mathop{\max}}\,f\left( x \right)=f\left( 1 \right)

.

\underset{\left( -\infty ;\,-1 \right)}{\mathop{\min }}\,f\left( x \right)=f\left( -1 \right)

.

\underset{\left( -1;\,1 \right]}{\mathop{\max}}\,f\left( x \right)=f\left( 0 \right)

.

Câu 4 (1đ):

Cho hàm số $y=2x-1+\dfrac{1}{x-2}$ . Tiệm cận xiên của đồ thị hàm số đã cho là

y=x-1

.

y=x-2

.

x=2

.

y=2x-1

.

Câu 5 (1đ):

Câu 6 (1đ):

Thời gian truy cập Internet mỗi buổi tối của một số học sinh được cho trong bảng sau:

Thời gian (phút)	Số học sinh
$\big[9,5 ; 12,5\big)$	$3$
$\big[12,5 ; 15,5\big)$	$12$
$\big[15,5 ; 18,5\big)$	$15$
$\big[18,5 ; 21,5\big)$	$24$
$\big[21,5 ; 24,5\big)$	$2$

Khoảng biến thiên của mẫu số liệu trên là

17

.

15

.

14

.

16

.

Câu 7 (1đ):

Trong không gian $Oxyz$ , cho hai vectơ $\overrightarrow{a}=(-1 ; 3 ;-3)$ và $\overrightarrow{b}=(2 ; 1 ;-2)$ . Tọa độ của vectơ $\overrightarrow{b}-\overrightarrow{a}$ là

(1 ; 4 ;-5).

(3 ;-2 ; 1).

(1 ;-2 ; 3).

(3 ; 2 ;-1).

Câu 8 (1đ):

Giá trị của tham số $m$ để giá trị lớn nhất của hàm số $y=x+\sqrt{4-{{x}^{2}}}+m$ bằng $3\sqrt{2}$ là

m=-\sqrt{2}

.

m=\dfrac{\sqrt{2}}{2}

.

m=\sqrt{2}

.

m=2\sqrt{2}

.

Câu 9 (1đ):

Có tất cả bao nhiêu giá trị khác nhau của tham số $m$ để đồ thị hàm số $y=\dfrac{x-1}{x^2+mx+4}$ có hai đường tiệm cận?

2

.

0

.

1

.

3

.

Câu 10 (1đ):

Kết quả đo chiều cao của $100$ cây keo ba năm tuổi tại một nông trường được cho ở bảng sau:

Chiều cao (m)	Số cây
$[8,4 ; 8,6)$	$5$
$[8,6 ; 8,8)$	$12$
$[8,8 ; 9,0)$	$25$
$[9,0 ; 9,2)$	$44$
$[9,2 ; 9,4)$	$14$

Phương sai của mẫu số liệu ghép nhóm đã cho (làm tròn đến chữ số hàng phần nghìn) bằng

0,023.

0,043.

0,455.

0,207.

Câu 11 (1đ):

Trong không gian với hệ trục tọa độ $O x y z$ , cho tam giác $A B C$ có ba đỉnh $A(-1 ; 1 ;-3)$ , $B (4 ; 2 ; 1)$ , $C( 3 ; 0 ; 5)$ . Tọa độ trọng tâm $G$ của tam giác $A B C$ là

G (2 ; 1 ; 1).

G (3 ; 1 ; 1).

G (1 ; 3 ; 2).

G(-1 ; 2 ; 1).

Câu 12 (1đ):

Hai chiếc khinh khí cầu bay lên từ cùng một địa điểm. Chiếc thứ nhất nằm cách điểm xuất phát $2$ km về phía nam và $1$ km về phía đông, đồng thời cách mặt đất $0,5$ km. Chiếc thứ hai nằm cách điểm xuất phát $1$ km về phía bắc và $1,5$ km về phía tây, đồng thời cách mặt đất $0,8$ km. Chọn hệ trục tọa độ $Oxyz$ với gốc $O$ đặt tại điểm xuất phát của hai khinh khí cầu, mặt phẳng $(Oxy)$ trùng với mặt đất với trục $Ox$ hướng về phía nam, $Oy$ hướng về phía đông, $Oz$ hướng thẳng đứng lên trời, đơn vị đo ki-lô-mét.

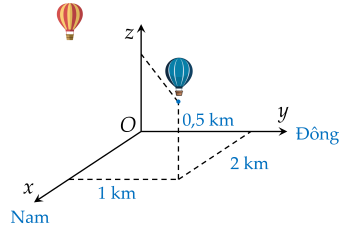
loading...

Khoảng cách giữa hai chiếc khinh khí cầu bằng

3,92

km.

3,82

km.

3,72

km.

3,62

km.

Câu 13 (1đ):

Trong không gian $Oxyz$ , cho $\overrightarrow{a}=( 1;\,2;\,-3)$ , $\overrightarrow{b}=\left( 3;\,1;\,5 \right)$ .

(Nhấp vào ô màu vàng để chọn đúng / sai)

a) $\overrightarrow{a}+\overrightarrow{b}=( 4;\,3;\,2)$ .
b) $2\overrightarrow{a}-3\overrightarrow{b}=( -7;\,1;\,21)$ .
c) $\overrightarrow{a}.\overrightarrow{b}=10$ .
d) $\cos \left( \overrightarrow{a},\overrightarrow{b} \right)=-\dfrac{\sqrt{10}}{7}$ .

Câu 14 (1đ):

Một loại thuốc được dùng cho một bệnh nhân và nồng độ thuốc trong máu của bệnh nhân được giám sát bởi bác sĩ. Biết rằng nồng độ thuốc trong máu của bệnh nhân sau khi tiêm vào cơ thể trong $t$ giờ được cho bởi hàm số có công thức $c(t)=\dfrac{t}{t^2+1}$ (mg/L).

(Nhấp vào ô màu vàng để chọn đúng / sai)

a) Nồng độ thuốc trong máu của bện nhân sau $3$ giờ là $c(3)=\dfrac{3}{10}$ (mg/L).
b) Đạo hàm của hàm số $c(t)=\dfrac{t}{t^2+1}$ là $c'(t)=\dfrac{1-t^2}{(t^2+1)^2}$ .
c) Nồng độ thuốc trong máu bệnh nhân tăng trong khoảng $t\in (0;\,2)$ .
d) Nồng độ thuốc trong máu của bệnh nhân cao nhất khi $t=\dfrac{1}{2}$ .

Câu 15 (1đ):

Cho hàm số $y=f\left(x \right)$ có bảng biến thiên như sau:

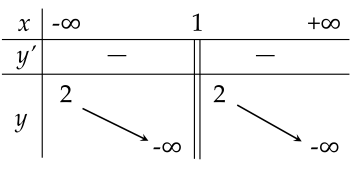
loading...

(Nhấp vào ô màu vàng để chọn đúng / sai)

a) Hàm số $y=f\left(x \right)$ liên tục và xác định trên $\mathbb{R}$ .
b) Phương trình $y=m$ có nghiệm với mọi $m$ .
c) Đồ thị hàm số $y=f\left(x \right)$ có $2$ tiệm cận đứng.
d) Đồ thị hàm số $y=\dfrac{1}{f\left(x \right)}$ có tất cả $3$ đường tiệm cận đứng và tiệm cận ngang.

Câu 16 (1đ):

Bảng sau đây cho biết chiều cao của các học sinh lớp $12A$ và lớp $12B$ .

Chiều cao (cm)	Số học sinh của lớp 12A	Số học sinh của lớp 12B
$[145;150)$	$1$	$0$
$[150;155)$	$0$	$0$
$[155;160)$	$10$	$15$
$[160;165)$	$12$	$9$
$[165;170)$	$12$	$10$
$[170;175)$	$5$	$8$

(Nhấp vào ô màu vàng để chọn đúng / sai)

a) So sánh hai khoảng biến thiên của hai mẫu số liệu trên, ta thấy mẫu số liệu về chiều cao của lớp $12A$ phân tán hơn lớp $12B$ .
b) Tứ phân vị thứ nhất của mẫu số liệu ghép nhóm về chiều cao của học sinh lớp $12A$ là $159,5$ .
c) Khoảng tứ phân vị của mẫu số liệu ghép nhóm về chiều cao của học sinh lớp $12B$ là $9,5$ .
d) So sánh hai khoảng tứ phân vị của hai mẫu số liệu ghép nhóm, ta thấy mẫu số liệu ghép nhóm về chiều cao của học sinh lớp $12A$ phân tán hơn của lớp $12B$ .

Câu 17 (1đ):

An tìm hiểu hàm lượng chất béo (đơn vị: g) có trong $100$ g mỗi loại thực phẩm. Sau khi thu thập dữ liệu về $60$ loại thực phẩm, An lập được bảng thống kê.

Hàm lượng chất béo (g)	Tần số
$[2;6)$	$2$
$[6;10)$	$6$
$[10;14)$	$10$
$[14;18)$	$13$
$[18;22)$	$16$
$[22;26)$	$13$

Tính khoảng tứ phân vị của mẫu số liệu trên. (Làm tròn đến chữ số thập phân thứ nhất)

Trả lời: .

Câu 18 (1đ):

Có bao nhiêu giá trị nguyên của tham số $m$ để hàm số $y=\dfrac{1}{3} x^{3} -\left(m+1\right)x^{2} +\left(m^{2} +2m\right)x-3$ nghịch biến trên khoảng $\left(0;1\right)$ ?

Trả lời:

Câu 19 (1đ):

Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình chữ nhật với $SA=4,\,AB=1,\,AD=2$ và $SA\bot \left(ABCD \right)$ . Gọi $M$ là trung điểm của $AB$ . Tính góc giữa hai vectơ $\overrightarrow{SC}$ và $\overrightarrow{DM}$ . (làm tròn đến đơn vị độ)

loading...

Trả lời: $^\circ$

Câu 20 (1đ):

Một con cá hồi bơi ngược dòng để vượt một khoảng cách là $300$ km. Vận tốc của dòng nước là $6$ km/h. Nếu vận tốc bơi của cá khi nước đứng yên là $v$ (km/h) thì năng lượng tiêu hao của cá trong $t$ giờ được cho bởi công thức: $E(v) = cv^3 t$ . Trong đó $c$ là một hằng số, $E$ được tính bằng jun. Tìm vận tốc bơi đơn vị km/h của cá khi nước đứng yên để năng lượng tiêu hao là ít nhất.

Trả lời:

Câu 21 (1đ):

Có bao nhiêu giá trị nguyên của tham số $m$ để đồ thị hàm số $y=3x+\dfrac{mx}{\sqrt{{{x}^{2}}+3}}$ có các điểm cực trị nằm trong hình tròn tâm $O$ , bán kính $R=\sqrt{130}$ ?

Trả lời:

Câu 22 (1đ):

Cho hàm số $y=\dfrac{2x-4}{x-1}$ có đồ thị $\left(C \right)$ và đường thẳng $\Delta: \, 2x+y-m=0$ . Gọi $S$ là tổng tất cả các giá trị của tham số $m$ để đường thẳng $\Delta$ cắt đồ thị $\left(C \right)$ tại hai điểm $A,\, B$ phân biệt, đồng thời trung điểm của đoạn $AB$ nằm trên đường tròn có tâm $I\left(1;-1 \right)$ , bán kính $R=2$ . Tính $S$ (ghi kết quả dưới dạng số thập phân).

Trả lời:

Bài học cùng chủ đề

Đề kiểm tra học kì I (đề số 3) SVIP

Yêu cầu đăng nhập!

Bài học cùng chủ đề

Báo cáo học liệu

Mua học liệu

Mua học liệu:

Số dư ví của bạn: 0 coin - 0 Xu

Nếu mua học liệu này bạn sẽ bị trừ: 0 coin\Xu

Để nhận Coin\Xu, bạn có thể:

Chi tiết xem tại đây

Thông tin của bạn

Đề kiểm tra học kì I (đề số 3) SVIP

Yêu cầu đăng nhập!

Truy vết IP log

Báo lỗi câu hỏi

Các khóa học có thể bạn quan tâm

Yêu cầu VIP