Đề kiểm tra học kì I (đề số 2)

Câu 1 (1đ):

Nghiệm của phương trình $\cos x=\dfrac12$ là

x=\pm \dfrac{\pi }{4}+k2\pi

,

k \in \mathbb{N}

.

x=\pm \dfrac{\pi }{6}+k2\pi

,

k \in \mathbb{N}

.

x=\pm \dfrac{\pi }{2}+k2\pi

,

k \in \mathbb{N}

.

x=\pm \dfrac{\pi }{3}+k2\pi

,

k \in \mathbb{N}

.

Câu 2 (1đ):

Cho cấp số cộng $(u_n)$ có $u_1=1,\, d=-4$ . Giá trị $u_3$ bằng

7

.

5

.

-5

.

-7

.

Câu 3 (1đ):

Khảo sát về thời gian (phút) đi từ nhà đến nơi làm việc của một số nhân viên trong một công ty như sau.

Thời gian (phút)	Số nhân viên
$\big[15 \, ; \, 20\big)$	$6$
$\big[20 \, ; \, 25\big)$	$14$
$\big[25 \, ; \, 30\big)$	$25$
$\big[30 \, ; \, 35\big)$	$37$
$\big[35 \, ; \, 40\big)$	$21$
$\big[40 \, ; \, 45\big)$	$13$
$\big[45 \, ; \, 50\big)$	$9$

Khẳng định nào sau đây sai?

Số nhân viên được khảo sát là

125

.

Bảng trên có

7

nhóm.

Độ dài nhóm

\big[ 15;20 \big)

là

6

.

Tần số của nhóm

\big[ 20;\,25 \big)

là

14

.

Câu 4 (1đ):

Câu 5 (1đ):

Trong không gian, mệnh đề nào sau đây đúng?

Phép chiếu song song biến hai đường thẳng cắt nhau thành hai đường thẳng cắt nhau.

Phép chiếu song song biến hai đường thẳng cắt nhau thành hai đường thẳng cắt nhau hoặc trùng nhau.

Phép chiếu song song biến hai đường thẳng cắt nhau thành hai đường thẳng song song.

Phép chiếu song song biến hai đường thẳng cắt nhau thành hai đường thẳng trùng nhau.

Câu 6 (1đ):

Khẳng định nào sau đây sai?

A

Nếu một đường thẳng cắt một trong hai mặt phẳng song song thì sẽ cắt mặt phẳng còn lại.

B

Nếu hai mặt phẳng song song thì mọi đường thẳng nằm trên mặt phẳng này đều song song với mặt phẳng kia.

C

Nếu mặt phẳng

(P)

chứa hai đường thẳng cùng song song với mặt phẳng

(Q)

thì

(P)

và

(Q)

song song với nhau.

D

Nếu hai mặt phẳng

(P)

và

(Q)

song song với nhau thì mặt phẳng

(R)

đã cắt

(P)

đều phải cắt

(Q)

và các giao tuyến của chúng song song nhau.

Câu 7 (1đ):

Giá trị của $\lim 5^n$ là

-\infty

.

+\infty

.

2

.

-2

.

Câu 8 (1đ):

Cho cấp số nhân $(u_n)$ có $\left\{ \begin{aligned} & u_2+u_4=60 \\ & u_3+u_5=180 \\ \end{aligned} \right.$ . Số hạng đầu của cấp số nhân là

6

.

5

.

3

.

2

.

Câu 9 (1đ):

Giới hạn $\underset{x\to 2}{\mathop{\lim}} \dfrac{x-2}{x^2-4}$ bằng

\dfrac14

.

2

.

4

.

0

.

Câu 10 (1đ):

Cho hàm số $y=f(x)=\left\{ \begin{aligned} & \dfrac{2-\sqrt{x+3}}{x^2-1} \, \, khi \, \, x\ne 1 \\ & \dfrac18 \, \, khi \, \, x=1 \\ \end{aligned} \right.$ . Giá trị $\underset{x \to 1^-}{\mathop{\lim}}f(x)$ bằng

-\dfrac18

.

+\infty

.

\dfrac18

.

0

.

Câu 11 (1đ):

$\underset{x \to +\infty }{\mathop{\lim}}(\sqrt{x^2-10x+5}-x)$ bằng

-5

.

-10

.

10

.

5

.

Câu 12 (1đ):

Cho hàm số $y = f(x)=\left\{ \begin{aligned} & \dfrac{\sqrt{2x+1}-\sqrt{x+5}}{x-4} \, \, khi \, \, x \ne 4 \\ & a+2 \, \, khi \, \, x=4 \\ \end{aligned} \right.$ . Tất cả các giá trị thực của tham số $a$ để hàm số liên tục tại $x_0=4$ là

a=3

.

a=2

.

a=-\dfrac{11}{6}

.

a=\dfrac{5}{2}

.

Câu 13 (1đ):

Cho dãy số $(u_n)$ có số hạng tổng quát $u_n=\dfrac{n}{4^n}$ .

(Nhấp vào ô màu vàng để chọn đúng / sai)

a) Ta có $u_n=\dfrac{n}{4^n}<0, \, \forall n \in \mathbb{N}^*$ .
b) Ta có $\dfrac{u_{n+1}}{u_n}<1, \, \forall n\ge 1$ .
c) Ta có $u_{2 \, 024}<u_{2 \, 023}$ .
d) Dãy số $(u_n)$ là dãy số tăng.

Câu 14 (1đ):

Số cuộc điện thoại một người thực hiện mỗi ngày trong $30$ ngày được lựa chọn ngẫu nhiên được thống kê trong bảng sau:

Số cuộc gọi	Số ngày
$\big[2,5 \, ; \, 5,5\big)$	$5$
$\big[5,5 \, ; \, 8,5\big)$	$13$
$\big[8,5 \, ; \, 11,5\big)$	$7$
$\big[11,5 \, ; \, 14,5\big)$	$3$
$\big[14,5 \, ; \, 17,5\big)$	$2$

(Nhấp vào ô màu vàng để chọn đúng / sai)

a) Số cuộc gọi trung bình mỗi ngày là $8,1.$
b) Nhóm chứa mốt là $\big[5,5;8,5\big)$ .
c) Mốt của mẫu số liệu ghép nhóm là $M_0 \approx 7,21.$
d) Người đó thực hiện tối đa khoảng $8$ cuộc gọi mỗi ngày.

Câu 15 (1đ):

Cho hình chóp $S.ABCD$ có đáy là hình bình hành. Gọi $O$ là giao điểm của $AC$ và $BD$ ; $M$ , $N$ lần lượt là trung điểm của $SB$ , $SD$ ; $P$ thuộc đọan $SC$ và không là trung điểm của $SC$ .

(Nhấp vào ô màu vàng để chọn đúng / sai)

a) Giao tuyến của hai mặt phẳng $(SAC)$ và $(SBD)$ là $SO$ .
b) Giao điểm $E$ của đường thẳng $SO$ và mặt phẳng $(MNP)$ là giao điểm của $MN$ và $SO$ .
c) Giao điểm $Q$ đường thẳng $SA$ và mặt phẳng $(MNP)$ là giao điểm của $PE$ và $SO$ .
d) Gọi $I$ , $J$ , $K$ lần lượt là giao điểm của $QM$ và $AB$ , $QP$ và $AC$ , $QN$ và $AD$ . Khi đó, $I$ , $J$ , $K$ thẳng hàng.

Câu 16 (1đ):

Trong hồ có chứa $6 \, 000$ lít nước ngọt (có nồng độ muối xem như bằng $0$ ). Người ta bơm nước biển có nồng độ muối là $30$ gam/lít vào hồ với tốc độ $15$ lít/phút. Biết rằng, nồng độ muối trong dung dịch được tính bằng công thức $C=\dfrac{m}{V}$ .

(Nhấp vào ô màu vàng để chọn đúng / sai)

a) Sau thời gian $t$ (phút), lượng nước được bơm vào hồ là $V(t)=15t$ (lít).
b) Khối lượng muối được bơm vào hồ sau thời gian $t$ (phút) là $m=450t$ (g).
c) Nồng độ muối trong hồ sau thời gian $t$ phút là $C(t)=\dfrac{15t}{6 \, 000+450t}$ .
d) Khi thời gian $t$ phút càng lớn, nồng độ muối trong hồ sẽ càng cao nhưng không vượt quá $C(t)=15$ (g/lít).

Câu 17 (1đ):

Trên nóc một tòa nhà có một cột ăng-ten cao $5$ m. Từ vị trí quan sát $A$ cao $7$ m so với mặt đất, có thể nhìn thấy đỉnh $B$ và chân $C$ của cột ăng-ten dưới góc $\alpha$ và $\beta$ so với phương nằm ngang.

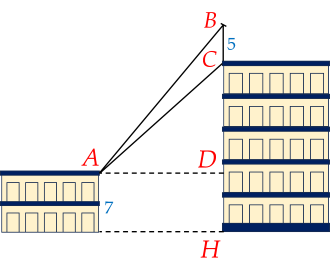
loading...

Biết chiều cao của toà nhà là $18,9$ m, hai toà nhà cách nhau $10$ m. Tính góc $\alpha = \widehat{BAD}$ (làm tròn kết quả đến hàng đơn vị theo đơn vị độ).

Trả lời:

Câu 18 (1đ):

Nguời ta thiết kế một cái tháp gồm $10$ tầng theo cách: Diện tích bề mặt trên của mỗi tầng bằng nửa diện tích bề mặt trên của tầng ngay bên dưới và diện tích bề mặt của tầng $1$ bằng nửa diện tích bề mặt đế tháp. Biết diện tích bề mặt đế tháp là $12 \, 288$ m $^2$ , tính diện tích bề mặt trên cùng của tháp (đơn vị mét vuông).

Trả lời:

Câu 19 (1đ):

Khảo sát số lần sử dụng Facebook của một người thực hiện mỗi ngày trong $30$ ngày được lựa chọn ngẫu nhiên được thống kê trong bảng sau:

Số lần sử dụng facebook	Số ngày
$\big[3 \, ; \, 5\big]$	$2$
$\big[6 \, ; \, 8\big]$	$5$
$\big[9 \, ; \, 11\big]$	$11$
$\big[12 \, ; \, 14\big]$	$8$
$\big[15 \, ; \, 17\big]$	$4$

Tìm mốt của mẫu số liệu ghép nhóm trên?

Trả lời:

Câu 20 (1đ):

Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình bình hành tâm $O$ . Gọi $M$ , $N$ lần lượt là trung điểm của các cạnh $CD$ và $SD$ . Biết rằng mặt phẳng $(BMN)$ cắt đường thẳng $SA$ tại $P$ . Tỉ số $\dfrac{SP}{SA}$ bằng bao nhiêu? (Làm tròn kết quả đến hàng trăm)

Trả lời:

Câu 21 (1đ):

Phương trình $\dfrac{5}{x-2}+\dfrac{\sqrt{3}}{x-\sqrt{5}}+\dfrac{2 \, 025}{x-1}=0$ có bao nhiêu nghiệm?

Trả lời:

Câu 22 (1đ):

Một hãng taxi đưa ra giá cước $T(x)$ (đồng) khi đi quãng đường $x$ (km) cho loại xe 4 chỗ như sau: $T(x)=\left\{ \begin{aligned} & 10 \, 000+a \,\,khi\,\, 0\lt x \le 0,7 \\ & 11\,000+15\,100.(x-0,7) \,\,khi\,\, 0,7\lt x\le 30 \\ & 453\,430+12\,000.(x-30) \,\,khi\,\, x>30 \\ \end{aligned} \right.$ . Để hàm số $T(x)$ liên tục tại $x=0,7$ thì giá trị của $a$ là bao nhiêu?

Trả lời:

Bài học cùng chủ đề

Đề kiểm tra học kì I (đề số 2) SVIP

Yêu cầu đăng nhập!

Bài học cùng chủ đề

Báo cáo học liệu

Mua học liệu

Mua học liệu:

Số dư ví của bạn: 0 coin - 0 Xu

Nếu mua học liệu này bạn sẽ bị trừ: 0 coin\Xu

Để nhận Coin\Xu, bạn có thể:

Chi tiết xem tại đây

Thông tin của bạn

Đề kiểm tra học kì I (đề số 2) SVIP

Yêu cầu đăng nhập!

Truy vết IP log

Báo lỗi câu hỏi

Các khóa học có thể bạn quan tâm

Yêu cầu VIP