Ta có hình vẽ như sau:
Gọi bán kính mặt đáy của cốc rượu là \(r\)
Gọi bán kính mặt đáy của lượng rượu là \(r_1\) 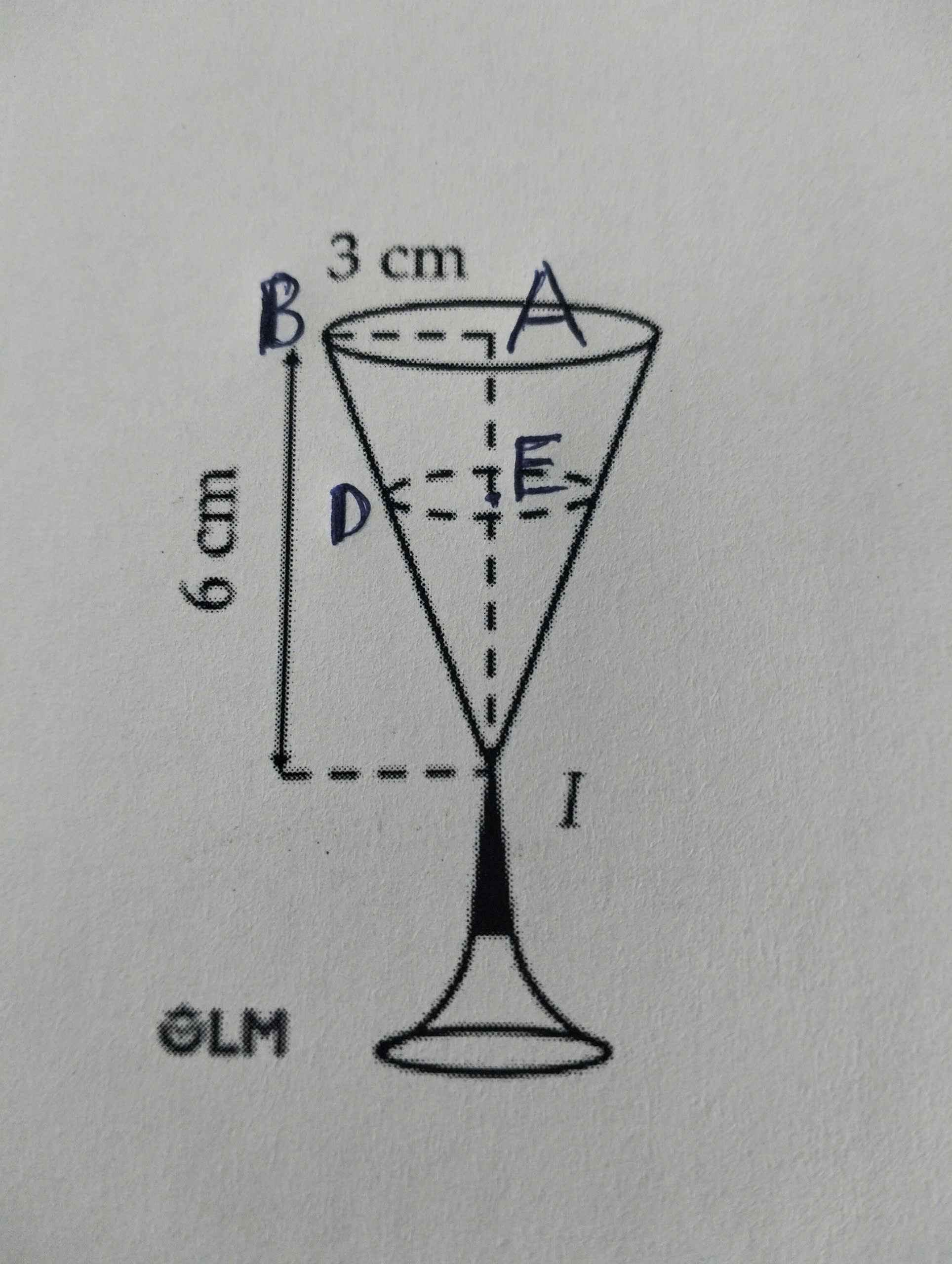
Gọi chiều cao của cốc rượu là \(h\)
Gọi chiều cao của lượng rượu là \(h_1\)
Gọi thể tích của cốc rượu là \(V\)
Gọi thể tích của lượng rượu là \(V_1\)
Áp dụng hệ quả của định lí Thales vào tam giác ABI có ED // AB, ta được:
\(\dfrac{h_1}{h}=\dfrac{r_1}{r}=>\dfrac{h_1}{6}=\dfrac{r_1}{3}=>r_1=\dfrac{1}{2}h_1\)
Ta có
\(=>V_1=V.\dfrac{1}{2}\)
\(=>\dfrac{1}{3}.\Pi.r_1^2.h_1=\dfrac{1}{3}.\Pi.3^2.6.\dfrac{1}{2}\)
\(=>\dfrac{1}{3}r_1^2.h_1=\dfrac{1}{3}9.6.\dfrac{1}{2}\)
\(=>\dfrac{1}{3}.\left(\dfrac{1}{2}h_1\right)^2.h_1=3.6.\dfrac{1}{2}\)
\(=>\dfrac{1}{3}.\dfrac{1}{2}^2.h_1^2.h_1=18.\dfrac{1}{2}\)
\(=>\dfrac{1}{3}.\dfrac{1}{4}.h_1^3=9\)
\(=>\dfrac{1}{12}.h_1^3=9\)
\(=>h_1^3=9:\dfrac{1}{12}\)
\(=>h_1^3=108\)
\(=>h_1=\sqrt[3]{108}\)
Vậy chiều cao của lượng rượu trong cốc rượu là \(\sqrt[3]{108}\) cm









