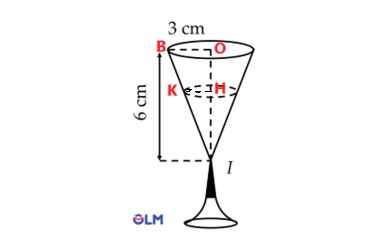
Gọi H, O lần lượt là tâm của mặt đáy hình nón chứa rượu và cốc rượu

HK, OB lần lượt là bán kính đáy của hình nón chứa rượu và cốc rượu

Xét △\(IOB\) có \(HK\)//\(OB\) (HK, OB cùng vuông góc với IO)

Áp dụng hệ quả định lí Ta-lét ta có:

\(\dfrac{IH}{IO}=\dfrac{HK}{OB}\Rightarrow\dfrac{IH}{6}=\dfrac{HK}{3}\Rightarrow HK=\dfrac{1}{2}IH\)   (*)

Thể tích cốc rượu là: \(V_1=\dfrac{1}{3}\Pi.IO.OB^2=\dfrac{1}{3}\Pi.6.3^2=18\Pi\left(cm^3\right)\)

Thể tích của phần chứa rượu trong cốc là: \(V_2=\dfrac{1}{3}\Pi.IH.HK^2\left(cm^3\right)\) (**)

Thay (*) vào (**) ta được: \(V_2=\dfrac{1}{3}\Pi.IH.\left(\dfrac{IH}{2}\right)^2=\dfrac{1}{12}\Pi.IH^3\left(cm^3\right)\)

Theo bài ra ta có:

\(V_2=\dfrac{1}{2}V_1\Rightarrow\dfrac{1}{12}\Pi.IH^3=\dfrac{1}{2}.18\Pi\\ \Rightarrow\dfrac{1}{12}IH^3=9\Rightarrow IH^3=12.9=108\\ \Rightarrow IH=\sqrt[3]{108}\left(cm\right)\)

Vậy để rót được nửa cốc rượu thì chiều cao của lượng rượu trong cốc bằng \(\sqrt[3]{108}cm\).