Nội dung tài liệu
1. TIÊN ĐỀ EUCLID VỀ ĐƯỜNG THẲNG SONG SONG
Chúng ta thừa nhận tính chất sau mang tên "Tiên đề Euclid":
Qua một điểm ở ngoài một đường thẳng, chỉ có một đường thẳng song song với đường thẳng đó.

Nhận xét: Nếu diểm $M$ nằm ngoài đường thẳng $a$ thì đường thẳng $b$ đi qua $M$ và song song với $a$ là duy nhất.
Chú ý: Từ tiên đề Euclid ta suy ra được: Nếu một đường thẳng cắt một trong hai đường thẳng song song thì nó cũng cắt đường thẳng còn lại.
2. TÍNH CHẤT CỦA HAI ĐƯỜNG THẲNG SONG SONG
Nếu một đường thẳng cắt hai đường thẳng song song thì:
- Hai góc so le trong bằng nhau;
- Hai góc đồng vị bằng nhau.
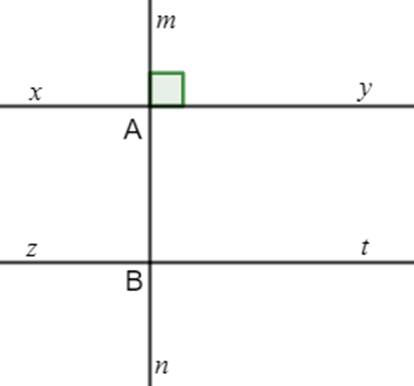
Ví dụ: Cho hình vẽ sau, biết $xy$ // $zt$ và \(\widehat{BAy}=60^0\). Tính số đo các góc \(\widehat{ABz}\) và \(\widehat{tBn}\).

Giải
Ta có $xy$ // $zt$, suy ra \(\widehat{ABz}=\widehat{BAy}\) (hai góc so le trong).
Do đó \(\widehat{ABz}=60^0\).
Cũng từ $xy$ // $zt$ suy ra \(\widehat{tBn}=\widehat{ABy}\) (hai góc đồng vị).
Vậy \(\widehat{tBn}=60^0\).
Nhận xét:
Một đường thẳng vuông góc với một trong hai đường thẳng song song thì nó cũng vuông góc với đường thẳng kia.
Hai đường thẳng phân biệt cùng song song với một đường thẳng thứ ba thì chúng song song với nhau.

