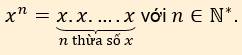Tài liệu liên quan
Nội dung tài liệu
I. PHÉP TÍNH LŨY THỪA VỚI SỐ MŨ TỰ NHIÊN
Lũy thừa bậc \(n\) của một số hữu tỉ \(x\), kí hiệu là \(x^n\), là tích của \(n\) thừa số \(x\):
Chú ý:
\(x^n\) đọc là "\(x\) mũ \(n\)" hoặc "\(x\) lũy thừa \(n\)" hoặc "lũy thừa bậc \(n\) của \(x\)";
\(x^2\) còn được gọi là "\(x\) bình phương" hay "bình phương của \(x\)";
\(x^3\) còn được gọi là "\(x\) lập phương" hay "lập phương của \(x\)".
Ví dụ: Viết mỗi tích sau dưới dạng một lũy thừa:
a) \(\dfrac{-4}{3}.\dfrac{-4}{3}.\dfrac{-4}{3}\);
b) \(\left(-0,5\right).\left(-0,5\right).\left(-0,5\right).\left(-0,5\right).\left(-0,5\right)\).
Giải
a) \(\dfrac{-4}{3}.\dfrac{-4}{3}.\dfrac{-4}{3}=\left(\dfrac{-4}{3}\right)^2\).
b) \(\left(-0,5\right).\left(-0,5\right).\left(-0,5\right).\left(-0,5\right).\left(-0,5\right)=\left(-0,5\right)^5\).
Lưu ý:
Để viết lũy thừa bậc \(n\) của phân số \(\dfrac{a}{b}\), ta phải viết \(\dfrac{a}{b}\) trong dấu ngoặc ( ), tức là \(\left(\dfrac{a}{b}\right)^n\).