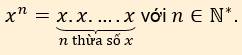Nội dung tài liệu
I. PHÉP TÍNH LŨY THỪA VỚI SỐ MŨ TỰ NHIÊN
Lũy thừa bậc \(n\) của một số hữu tỉ \(x\), kí hiệu là \(x^n\), là tích của \(n\) thừa số \(x\):
Chú ý:
\(x^n\) đọc là "\(x\) mũ \(n\)" hoặc "\(x\) lũy thừa \(n\)" hoặc "lũy thừa bậc \(n\) của \(x\)";
\(x^2\) còn được gọi là "\(x\) bình phương" hay "bình phương của \(x\)";
\(x^3\) còn được gọi là "\(x\) lập phương" hay "lập phương của \(x\)".
Ví dụ: Viết mỗi tích sau dưới dạng một lũy thừa:
a) \(\dfrac{-4}{3}.\dfrac{-4}{3}.\dfrac{-4}{3}\);
b) \(\left(-0,5\right).\left(-0,5\right).\left(-0,5\right).\left(-0,5\right).\left(-0,5\right)\).
Giải
a) \(\dfrac{-4}{3}.\dfrac{-4}{3}.\dfrac{-4}{3}=\left(\dfrac{-4}{3}\right)^2\).
b) \(\left(-0,5\right).\left(-0,5\right).\left(-0,5\right).\left(-0,5\right).\left(-0,5\right)=\left(-0,5\right)^5\).
Lưu ý:
Để viết lũy thừa bậc \(n\) của phân số \(\dfrac{a}{b}\), ta phải viết \(\dfrac{a}{b}\) trong dấu ngoặc ( ), tức là \(\left(\dfrac{a}{b}\right)^n\).