Cho hình tam giác ABC, trên cạnh BC lấy 1 điểm D sao cho BD = \(\frac{1}{2}\) DC., trên AC lấy trung điểm E, nối A với D, D với E. So sánh diện tích các hình tam giác ADB, ADE, DEC
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
15 tháng 6 2023
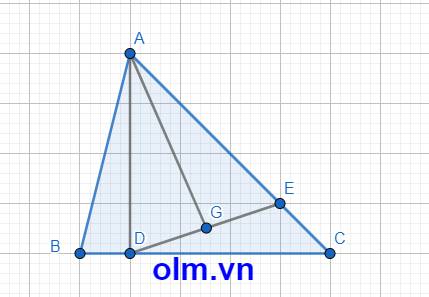
SADE = 2\(\times\)SAGE ( vì hai tam giác có chung chiều cao hạ từ đỉnh A xuống đáy DE và DE = 2\(\times\) GE )
⇒ SADE = 36 \(\times\) 2 = 72 (cm2)
SADE = \(\dfrac{3}{4}\)\(\times\)SADC (vì hai tam giác có chung chiều cao hạ từ Đỉnh D xuống đáy AC và AE = \(\dfrac{3}{4}\)AC)
⇒ SACD = 72 : \(\dfrac{3}{4}\) = 96 (cm2)
DC = BC - BD = BC - \(\dfrac{1}{5}\)BC = \(\dfrac{4}{5}\)BC
SADC = \(\dfrac{4}{5}\)SABC (vì hai tam giác có chung chiều cao hạ từ đỉnh A xuống đáy BC và DC = \(\dfrac{4}{5}\)BC)
⇒ SABC = 96 : \(\dfrac{4}{5}\) = 120 (cm2)
Tỉ số phần trăm diện tích tam giác ADE và diện tích tam giác ABC là:
72 : 120 = 0,6
0,6 = 60%
Đáp số: 60%
22 tháng 5 2023
a: S ABE=S EBD=1/2*S ABD
DC=1/2DB
nên S ADC=1/2*S ABD
=>S ABE=S EBD=S ADC
b: S ABC=3/2*24=36cm2
BT
10 tháng 1 2020
Trl :
Ta có :
\(S_{ABD}=S_{ADC}\times2\) ( Vì có chung chiều cao hạ từ A xuống BD )
\(S_{EBD}=S_{EDC}\times2\) ( Vì có chung chiều cao hạ từ E xuống BC )
Suy ra : \(S_{BAE}=S_{CAE}\times2\)( Hiệu diện tích )